speed problem solving examples

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 8: Rational Expressions

8.8 Rate Word Problems: Speed, Distance and Time

Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .

[latex]r\cdot t=d[/latex]

For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.

The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:

The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.

Example 8.8.1

Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ km/h} \end{array}[/latex]

This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.

Example 8.8.2

Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?

The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:

[latex]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}[/latex]

This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.

Example 8.8.3

Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?

The distance travelled by both is the same. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]

This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.

Example 8.8.4

On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?

[latex]\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}[/latex]

This means that the time spent travelling at 40 km/h was 0.5 h.

Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.

For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.

• A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
• Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
• Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
• Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
• A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
• Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
• A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
• A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?

Solve Questions 9 to 22.

• A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
• A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
• A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
• As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
• Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
• A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
• A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
• A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
• Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
• Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
• Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
• Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
• On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
• Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.

Answer Key 8.8

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Problems on Calculating Speed | Speed Questions and Answers

Solve different types of problems on calculating speed and get acquainted with various models of questions asked in your exams. Be aware of the Formula to Calculate and Relationship between Speed Time and Distance. Practice Speed Problems on a regular basis so that you can be confident while attempting the exams. We even provided solutions for all the Questions provided and explained everything in detail for better understanding. Try to solve the Speed Questions on your own and then cross-check where you are lagging.

We know the Speed of the Object is nothing but the distance traveled by the object in unit time.

Formula to find out Speed is given by Speed = Distance/Time

Word Problems on Calculating Speed

1.  A man walks 25 km in 6 hours. Find the speed of the man?

Solution: Distance traveled = 25 km Time taken to travel = 6 hours Speed of Man = Distance traveled/Time taken = 25km/6hr = 4.16 km/hr Therefore, a man travels at a speed of 4.16 km/hr

2. A car covers a distance of 420 m in 1 minute whereas a train covers 70 km in 30 minutes. Find the ratio of their speeds?

Solution: Speed of the Car = Distance Traveled/Time Taken = 420m/60 sec = 7 m/sec

Speed of the Train = Distance Traveled/Time Taken = 70 km/1/2 hr = 140 km/hr

To convert it into m/sec multiply with 5/18 = 140*5/18 = 38.8 m/sec = 39 m/sec (Approx) Ratio of Speeds = 7:39

3. A car moves from A to B at a speed of 70 km/hr and comes back from B to A at a speed of 40 km/hr. Find its average speed during the journey?

Solution: Since the distance traveled is the same the Average Speed= (x+y)/2 where x, y are two different speeds Substitute the Speeds in the given formula Average Speed = (70+40)/2 = 110/2 = 55 km/hr The Average Speed of the Car is 55 km/hr

4. A bus covers a certain distance in 45 minutes if it runs at a speed of 50 km/hr. What must be the speed of the bus in order to reduce the time of journey by 20 minutes?

Solution: Speed = Distance/Time 50 = x/3/4 50 = 4x/3 4x = 150 x = 150/4 = 37.5 km

Now by applying the same formula we can find the speed

Now, time = 40 mins or 0.66 hr since the journey is reduced by 20 mins

S = Distance/Time = 37.5/0.66 = 56.81 km/hr

5. Ram traveled 200 km in 3 hours by train and then traveled 140 km in 3 hours by car and 5 km in 1/2 hour by cycle. What is the average speed during the whole journey?

Solution: Distance traveled by Train is 200 km in 3 hours Distance Traveled by Car is 140 km in 3 hours Distance Traveled by Cycle is 5 km in 1/2 hour Average Speed = Total Distance/Total Time = (200+140+5)/(3+3+1/2) = 345/6 1/2 = 345/(13/2)” = 345*2/13 = 53.07 km/hr

6. A train covers 150 km in 3 hours. Find its speed?

Solution: Speed = Distance/Time = 150 km/3 hr = 50 km/hr Therefore, Speed of the Train is 50 km/hr.

Leave a Comment Cancel Reply

You must be logged in to post a comment.

Problems on Calculating Speed

Here we will learn to solve different types of problems on calculating speed.

We know, the speed of a moving body is the distance traveled by it in unit time.             

Formula to find out speed = distance/time

Word problems on calculating speed:

1.  A man walks 20 km in 4 hours. Find his speed.

Solution:            

Distance covered = 20 km

Time taken = 4 hours

We know, speed = distance/time            

                       = 20/4 km/hr

Therefore, speed = 5 km/hr

2. A car covers a distance of 450 m in 1 minute whereas a train covers 69 km in 45 minutes. Find the ratio of their speeds.

Speed of car = Distance covered/Time taken = 450/60 m/sec = 15/2

                                                            = 15/2 × 18/5 km/hr

                                                            = 27 km/hr

Distance covered by train = 69 km

Time taken = 45 min = 45/60 hr = 3/4 hr

Therefore, speed of trains = 69/(3/4) km/hr

                                    = 69/1 × 4/3 km/hr

                                    = 92 km/hr

Therefore, ratio of their speed i.e., speed of car/speed of train = 27/92 = 27 : 92

3. Kate travels a distance of 9 km from her house to the school by auto-rickshaw at 18 km/hr and returns on rickshaw at 15 km/hr. Find the average speed for the whole journey.

Time taken by Kate to reach school = distance/speed = 9/18 hr = 1/2 hr

Time taken by Kate to reach house to school = 9/15 = 3/5 hr

Total time of journey = (1/2 + 3/5) hr

Total time of journey = (5 + 6)/10 = 11/10 hr

Total distance covered = (9 + 9) km = 18 km

Therefore, average speed for the whole journey = distance/speed = 18/(11/10) km/hr

= 18/1 × 10/11 = (18 × 10)/(1 × 11) km/hr

                      = 180/11 km/hr

                      = 16.3 km/hr (approximately)

Speed of Train

Relationship between Speed, Distance and Time

Conversion of Units of Speed

Problems on Calculating Distance

Problems on Calculating Time

Two Objects Move in Same Direction

Two Objects Move in Opposite Direction

Train Passes a Moving Object in the Same Direction

Train Passes a Moving Object in the Opposite Direction

Train Passes through a Pole

Train Passes through a Bridge

Two Trains Passes in the Same Direction

Two Trains Passes in the Opposite Direction

8th Grade Math Practice From Problems on Calculating Speed to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

Share this page: What’s this?

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Worksheet on Yesterday, Today and Tomorrow | Sequence of the Week-days

Nov 25, 24 01:18 AM

Yesterday, Today and Tomorrow | Name of each Day of the Week

Nov 25, 24 01:09 AM

The Story about Seasons | Spring | Summer | Autumn | Winter

Nov 25, 24 12:48 AM

Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr

Nov 25, 24 12:17 AM

Time Duration |How to Calculate the Time Duration (in Hours & Minutes)

Nov 24, 24 11:01 PM

Worksheet on Conversion of Units of Speed

Worksheet on Calculating Time

Worksheet on Calculating Speed

Worksheet on Calculating Distance

Worksheet on Train Passes through a Pole

Worksheet on Train Passes through a Bridge  

Worksheet on Relative Speed

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

TIME SPEED AND DISTANCE PROBLEMS

Formulas .

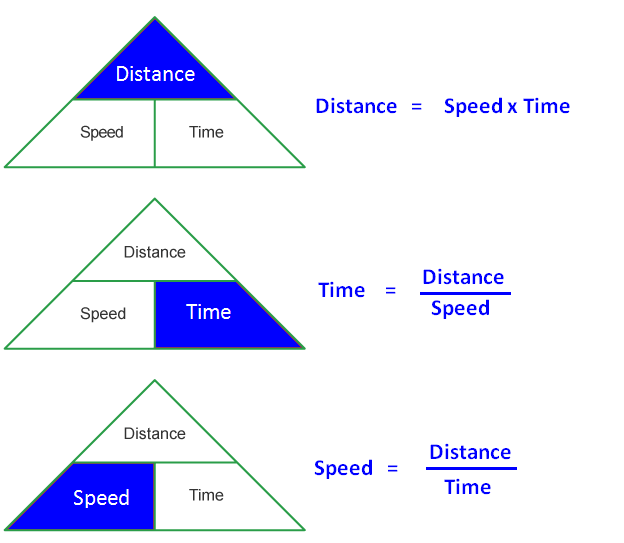
To know the shortcuts required to solve problems on time, speed and distance,

please click here

Problem 1 :

If a person drives his car in the speed 50 miles per hour, how far can he cover in 2.5 hours?

Given :  Speed is 50 miles per hour.

So, the distance covered in 1 hour is

Then, the distance covered in 2.5 hours is

= 2.5 ⋅ 50 miles

= 125 miles

So, the person can cover 125 miles of distance in 2.5 hours.

Problem 2 :

If a person travels at a speed of 40 miles per hour. At the same rate, how long will he take to cover 160 miles distance?

Given :  Speed is 40 miles per hour.

The formula to find the time when distance and speed are given is

Time taken to cover the distance of 160 miles is

So, the person will take 4 hours to cover 160 miles distance at the rate of 40 miles per hour.

Problem 3 :

A person travels at a speed of 60 miles per hour. How far will he travel in 4.5 hours?

Given :  Speed is 60 miles per hour.

The distance covered in 1 hour is

Then, the distance covered in 4.5 hours is

= 4.5 ⋅ 60 miles

= 270 miles

So, the person will travel 270 miles distance in 4.5 hours.

Problem 4 :

A person travels at a speed of 60 kms per hour. Then how many meters can he travel in 5 minutes?

Given :  Speed is 60 kms per hour.

The distance covered in 1 hour or 60 minutes is

= 60 ⋅ 1000 meters

= 60000 meters

Then the distance covered in 1 minute is

The distance covered in 5 minutes is

= 5 ⋅ 1000

= 5000 meters

So, the person can cover 5000 meters distance in 5 minutes.

Problem 5 :

A person covers 108 kms in 3 hours. What is his speed in meter per second?

Given :  Distance is 108 kms and time is 3 hours.

The given distance in meters :

= 108 ⋅ 1000

= 108,000 meters

The given time in seconds :

= 3 ⋅ 60 minutes

= 180 minutes

= 180 ⋅ 60 seconds

= 10,800 seconds

The formula to find the speed is

Speed in meter per second is

= ¹⁰⁸⁰⁰⁰⁄₁₀₈₀₀

So, his speed in meter per second is 10.

Problem 6 :

A person covers 90 kms in 2 hours 30 minutes. Find the speed in meter per second.

Given :  Distance is 90 kms and time is 2 hrs 30 min.

= 90 ⋅ 1000

= 90,000 meters

= 2 hrs 30 min

= (120 + 30) min

= 150 minutes

= 150 ⋅ 60 seconds

= 9,000 seconds

= ⁹⁰⁰⁰⁰⁄₉₀₀₀

Problem 7 :

A person travels at the rate of 60 miles per hour and covers 300 miles in 5 hours. If he reduces his speed by 10 miles per hour, how long will he take to cover the same distance?

Original speed is 60 miles per hour.

If the speed is reduced by 10 miles per hour,  then the new speed is

= 50 miles per hour

Distance to be covered is 300 miles.

The formula to find time is

Time taken to cover 300 miles distance at the speed of 50 miles per hour is

So, if the person reduces his speed by 10 miles per hour, he will take 6 hours to cover 300 miles distance.

Problem 8 :

A person travels 50 kms per hour. If he increases his speed by 10 kms per hour, how many minutes will he take to cover 8000 meters?

Original speed is 50 kms per hour.

If the speed is increased by 10 kms per hour,  then the new speed is

= 60 kms per hour

Because, we have to find the time in minutes for the distance given in meters, let us change the speed from kms per hour into meters per minute.

1 hour ----> 60 kms

1 ⋅ 60 minutes ----> 60 ⋅ 1000 meters

60 minutes ----> 60000 meters

1 minute ----> ⁶⁰⁰⁰⁰⁄₆₀ meters

1 minute ----> 1000 meters

So, the speed is 1000 meters/minute.

Time = Distance/Speed

Time taken to cover 8000 meters distance at the speed of 1000 meters per minute is

= ⁸⁰⁰⁰⁄₁₀₀₀

= 8 minutes

So, if the person increases his speed by 10 kms per hour, he will take 8 minutes to cover 8000 meters distance.

Problem 9 :

A person can travel at the speed of 40 miles per hour. If the speed is increased by 50%, how long will it take to cover 330 miles?

Original speed is 40 miles per hour.

If the speed is increased by 50%, then the new speed is

= 150% of 40

= 1.5 ⋅ 40

= 60 miles per hour

Distance to be covered is 330 miles.

Time taken to cover 330 miles distance at the speed of 60 miles per hour is

= 5.5 hours

= 5 hrs 30 minutes

So, if the person is increased by 50%, it will take 5 hrs 30 minutes to cover 330 miles distance.

Problem 10 :

A person speed at a rate of 40 kms per hour. If he increases his speed by 20%, what is his new speed in meter per minute?

Original speed is 40 kms per hour

If the speed is increased by 20%, then the new speed is

= 120 % of 40

= 1.2 ⋅ 40

= 48 kms per hour

Now, let us change the speed from kms per hour into meters per minute.

1 hour ----> 48 kms

1 ⋅ 60 minutes ----> 48 ⋅ 1000 meters

60 minutes ----> 48,000 meters

1 minute ----> ⁴⁸⁰⁰⁰⁄₆₀ meters

1 minute ----> 800 meters

So, the speed is 800 meters/minute.

If the person increases his speed by 20%, his new speed will be 800 meter per minute.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Digital SAT Math Problems and Solutions (Part - 72)

Nov 23, 24 09:36 PM

SAT Math Resources (Videos, Concepts, Worksheets and More)

Nov 23, 24 10:01 AM

Digital SAT Math Problems and Solutions (Part - 76)

Nov 23, 24 09:45 AM

Watch how a non-IITian got 6 MBA admits + $250,000 in scholarships

Distance, Time and Speed Word Problems | GMAT GRE Maths

Before you get into distance, time and speed word problems, check out how you can add a little power to your resume by getting our mini-MBA certificate.  

Problems involving Time, Distance and Speed are solved based on one simple formula.

Distance = Speed * Time

Which implies →

Speed = Distance / Time   and

Time = Distance / Speed

Let us take a look at some simple examples of distance, time and speed problems.   Example 1. A boy walks at a speed of 4 kmph. How much time does he take to walk a distance of 20 km?

Time = Distance / speed = 20/4 = 5 hours.   Example 2. A cyclist covers a distance of 15 miles in 2 hours. Calculate his speed.

Speed = Distance/time = 15/2 = 7.5 miles per hour.   Example 3. A car takes 4 hours to cover a distance, if it travels at a speed of 40 mph. What should be its speed to cover the same distance in 1.5 hours?

Distance covered = 4*40 = 160 miles

Speed required to cover the same distance in 1.5 hours = 160/1.5 = 106.66 mph   Now, take a look at the following example:

Example 4. If a person walks at 4 mph, he covers a certain distance. If he walks at 9 mph, he covers 7.5 miles more. How much distance did he actually cover?

Now we can see that the direct application of our usual formula Distance = Speed * Time or its variations cannot be done in this case and we need to put in extra effort to calculate the given parameters.

Let us see how this question can be solved.

For these kinds of questions, a table like this might make it easier to solve.

  Let the distance covered by that person be ‘d’.

Walking at 4 mph and covering a distance ‘d’ is done in a time of ‘d/4’

IF he walks at 9 mph, he covers 7.5 miles more than the actual distance d, which is ‘d+7.5’.

He does this in a time of (d+7.5)/9.

Since the time is same in both the cases →

d/4 = (d+7.5)/9            →        9d = 4(d+7.5)   →        9d=4d+30        →        d = 6.

So, he covered a distance of 6 miles in 1.5 hours.   Example 5. A train is going at 1/3 of its usual speed and it takes an extra 30 minutes to reach its destination. Find its usual time to cover the same distance.

Here, we see that the distance is same.

Let us assume that its usual speed is ‘s’ and time is ‘t’, then

  s*t = (1/3)s*(t+30)      →        t = t/3 + 10      →        t = 15.

So the actual time taken to cover the distance is 15 minutes.

Note: Note the time is expressed in terms of ‘minutes’. When we express distance in terms of miles or kilometers, time is expressed in terms of hours and has to be converted into appropriate units of measurement.

Solved Questions on Trains

Example 1. X and Y are two stations which are 320 miles apart. A train starts at a certain time from X and travels towards Y at 70 mph. After 2 hours, another train starts from Y and travels towards X at 20 mph. At what time do they meet?

Let the time after which they meet be ‘t’ hours.

Then the time travelled by second train becomes ‘t-2’.

Distance covered by first train+Distance covered by second train = 320 miles

70t+20(t-2) = 320

Solving this gives t = 4.

So the two trains meet after 4 hours.   Example 2. A train leaves from a station and moves at a certain speed. After 2 hours, another train leaves from the same station and moves in the same direction at a speed of 60 mph. If it catches up with the first train in 4 hours, what is the speed of the first train?

Let the speed of the first train be ‘s’.

Distance covered by the first train in (2+4) hours = Distance covered by second train in 4 hours

Therefore, 6s = 60*4

Solving which gives s=40.

So the slower train is moving at the rate of 40 mph.  

Questions on Boats/Airplanes

For problems with boats and streams,

Speed of the boat upstream (against the current) = Speed of the boat in still water – speed of the stream

[As the stream obstructs the speed of the boat in still water, its speed has to be subtracted from the usual speed of the boat]

Speed of the boat downstream (along with the current) = Speed of the boat in still water + speed of the stream

[As the stream pushes the boat and makes it easier for the boat to reach the destination faster, speed of the stream has to be added]

Similarly, for airplanes travelling with/against the wind,

Speed of the plane with the wind = speed of the plane + speed of the wind

Speed of the plane against the wind = speed of the plane – speed of the wind

Let us look at some examples.

Example 1. A man travels at 3 mph in still water. If the current’s velocity is 1 mph, it takes 3 hours to row to a place and come back. How far is the place?

Let the distance be ‘d’ miles.

Time taken to cover the distance upstream + Time taken to cover the distance downstream = 3

Speed upstream = 3-1 = 2 mph

Speed downstream = 3+1 = 4 mph

So, our equation would be d/2 + d/4 = 3 → solving which, we get d = 4 miles.   Example 2. With the wind, an airplane covers a distance of 2400 kms in 4 hours and against the wind in 6 hours. What is the speed of the plane and that of the wind?

Let the speed of the plane be ‘a’ and that of the wind be ‘w’.

Our table looks like this:  

  4(a+w) = 2400 and 6(a-w) = 2400

Expressing one unknown variable in terms of the other makes it easier to solve, which means

a+w = 600 → w=600-a

Substituting the value of w in the second equation,

a-(600-a) = 400 → a = 500

The speed of the plane is 500 kmph and that of the wind is 100 kmph.  

More solved examples on Speed, Distance and Time

Example 1. A boy travelled by train which moved at the speed of 30 mph. He then boarded a bus which moved at the speed of 40 mph and reached his destination. The entire distance covered was 100 miles and the entire duration of the journey was 3 hours. Find the distance he travelled by bus.

Let the time taken by the train be ‘t’. Then that of bus is ‘3-t’.

The entire distance covered was 100 miles

So, 30t + 40(3-t) = 100

Solving which gives t=2.

Substituting the value of t in 40(3-t), we get the distance travelled by bus is 40 miles.

Alternatively, we can add the time and equate it to 3 hours, which directly gives the distance.

d/30 + (100-d)/40 = 3

Solving which gives d = 60, which is the distance travelled by train. 100-60 = 40 miles is the distance travelled by bus.   Example 2. A plane covered a distance of 630 miles in 6 hours. For the first part of the trip, the average speed was 100 mph and for the second part of the trip, the average speed was 110 mph. what is the time it flew at each speed?

Our table looks like this.

Assuming the distance covered in the 1 st part of journey to be ‘d’, the distance covered in the second half becomes ‘630-d’.

Assuming the time taken for the first part of the journey to be ‘t’, the time taken for the second half becomes ‘6-t’.

From the first equation, d=100t

The second equation is 630-d = 110(6-t).

Substituting the value of d from the first equation, we get

630-100t = 110(6-t)

Solving this gives t=3.

So the plane flew the first part of the journey in 3 hours and the second part in 3 hours.   Example 2. Two persons are walking towards each other on a walking path that is 20 miles long. One is walking at the rate of 3 mph and the other at 4 mph. After how much time will they meet each other?

  Assuming the distance travelled by the first person to be ‘d’, the distance travelled by the second person is ’20-d’.

The time is ‘t’ for both of them because when they meet, they would have walked for the same time.

Since time is same, we can equate as

d/3 = (20-d)/4

Solving this gives d=60/7 miles (8.5 miles approximately)

Then t = 20/7 hours

So the two persons meet after 2 6/7 hours.  

Practice Questions for you to solve

Problem 1: Click here

A boat covers a certain distance in 2 hours, while it comes back in 3 hours. If the speed of the stream is 4 kmph, what is the boat’s speed in still water?

A) 30 kmph B) 20 kmph C) 15 kmph D) 40 kmph

Answer 1: Click here

Explanation

Let the speed of the boat be ‘s’ kmph.

Then, 2(s+4) = 3(s-4) → s = 20

Problem 2: Click here

A cyclist travels for 3 hours, travelling for the first half of the journey at 12 mph and the second half at 15 mph. Find the total distance he covered.

A) 30 miles B) 35 miles C) 40 miles D) 180 miles

Answer 2: Click here

Since it is mentioned, that the first ‘half’ of the journey is covered in 12 mph and the second in 15, the equation looks like

(d/2)/12 + (d/2)/15 = 3

Solving this gives d = 40 miles

Watch an M7 MBA admit reveal his application strategy Mini-MBA | Start here | Success stories | Reality check | Knowledgebase | Scholarships | Services Serious about higher ed? Follow us:                

17 thoughts on “Distance, Time and Speed Word Problems | GMAT GRE Maths”

Meera walked to school at a speed of 3 miles per hour. Once she reached the school, she realized that she forgot to bring her books, so rushed back home at a speed of 6 miles per hour. She then walked back to school at a speed of 4 miles per hour. All the times, she walked in the same route. please explain above problem

When she walks faster the time she takes to reach her home and school is lower. There is nothing wrong with the statement. They never mentioned how long she took every time.

a man covers a distance on a toy train.if the train moved 4km/hr faster,it would take 30 min. less. if it moved 2km/hr slower, it would have taken 20 min. more .find the distance.

Let the speed be x. and time be y. A.T.Q, (x+4)(y-1/2)=d and (x-2)(y+1/3)=d. Equate these two and get the answer

Could you explain how ? you have two equations and there are 3 variables.

The 3rd equation is d=xy. Now, you have 3 equations with 3 unknowns. The variables x and y represent the usual speed and usual time to travel distance d.

Speed comes out to be 20 km/hr and the time taken is 3 hrs. The distance traveled is 60 km.

(s + 4) (t – 1/2)= st 1…new equotion = -1/2s + 4t = 2

(s – 2) (t + 1/3)= st 2…new equotion = 1/3s – 2t = 2/3

Multiply all by 6 1… -3s + 24t = 12 2… 2s – 12t = 4 Next, use elimination t= 3 Find s: -3s + 24t = 12 -3s + 24(3) = 12 -3s = -60 s= 20

st or distance = 3 x 20 = 60 km/h

It’s probably the average speed that we are looking for here. Ave. Speed= total distance/ total time. Since it’s harder to look for one variable since both are absent, you can use, 3d/ d( V2V3 + V1V3 + V1V2/ V1V2V3)

2 girls meenu and priya start at the same time to ride from madurai to manamadurai, 60 km away.meenu travels 4kmph slower than priya. priya reaches manamadurai and at turns back meeting meenu 12km from manamaduai. find meenu’s speed?

Hi, when the two girls meet, they have taken equal time to travel their respective distance. So, we just need to equate their time equations

Distance travelled by Meenu = 60 -12 = 48 Distance travelled by Priya = 60 + 12 = 72 Let ‘s’ be the speed of Meenu

Time taken by Meenu => t1 = 48/s Time taken by Priya => t2 = 72/(s+4)

t1=t2 Thus, 48/s = 72/(s+4) => 24s = 192 => s = 8Km/hr

A train can travel 50% faster than a car. Both start from point A at the same time and reach point B 75 KMS away from A at the same time. On the way, however the train lost about 12.5 minutes while stopping at the stations. The speed of the car is:

Let speed of the CAR BE x kmph.

Then, speed of the train = 3/2(x) .’. 75/x – 75/(3/2)x= 125/(10*60) — subtracting the times travelled by two them hence trains wastage time

therefore x= 120 kmph

A cyclist completes a distance of 60 km at the same speed throughout. She travels 10 km in one hour. She stops every 20 km for one hour to have a break. What are the two variables involved in this situation?

For the answer, not variables: 60km divided by 10km/h=6 hours 60 divided by 20= 3 hours 3 hours+6 hours= 9 hours Answer: 9 hours

Let the length of the train to prod past a point be the intrinsic distance (D) of the train and its speed be S. Its speed, S in passing the electric pole of negligible length is = D/12. The length of the platform added to the intrinsic length of the train. So, the total distance = D + 200. The time = 20 secs. The Speed, S = (D + 200)/20 At constant speed, D/12 = (D + 200)/20 Cross-multiplying, 20D = 12D + 200*12 20D – 12D = 200*12; 8D = 200*12 D = 200*12/8 = 300m. 4th Aug, 2018

Can anyone solve this? Nathan and Philip agree to meet up at the park at 5:00 pm. Nathan lives 300 m due north of the park, and Philip lives 500 m due west of the park. Philip leaves his house at 4:54 pm and walks towards the park at a pace of 1.5 m/s, but Nathan loses track of time and doesn’t leave until 4:59 pm. Trying to avoid being too late, he jogs towards the park at 2.5 m/s. At what rate is the distance between the two friends changing 30 seconds after Nathan has departed?

Leave a Comment Cancel reply

• The Basic math blog
• Member Login
• Pre-Algebra Lessons
• Pre-Algebra Word Problems
• Pre-Algebra Calculators
• Algebra Lessons
• Algebra Word Problems
• Algebra Proofs
• Advanced Algebra
• Algebra Calculators
• Geometry Lessons
• Geometry Word Problems
• Geometry Proofs
• Geometry Calculators
• Trigonometry Lessons
• Numeration System
• Basic Concepts of Set Theory
• Consumer Math
• Baseball Math
• Math for Nurses
• Statistics Made Easy
• High School Physics
• Basic Mathematics Store
• Math Vocabulary Quizzes
• SAT Math Prep
• Math Skills by Grade Level
• Ask an Expert
• Other Websites
• K-12 Worksheets
• Worksheets Generator
• Algebra Worksheets
• Geometry Worksheets
• Fun Online Math Games
• Pre-Algebra Games
• Math Puzzles
• Math Tricks

Speed word problems

The speed word problems to follow don't have complicated math equations at all. Instead, the focus is on understanding how to apply the concept of speed, distance, and time. 

Interesting speed word problems

Problem #1 : Calculate the average speed of a lion that runs 45 meters in 5 seconds . What could be some possible instantaneous speeds?

Solution:   The formula to get the average speed is 

The total distance is 45 meters, so d = 45 meters.

It took the lion 5 seconds to reach a distance of 45 meters.

The total time is 5 seconds, so t = 5.

Just plug these into the formula. 

d = 9 meters per second.

You could also write d = 9 m/s.

Some possible instantaneous speed for the lion could be the followings:

13 meters in 1 second      v = 13 m/s

9 meters in 1 second        v  = 9 m/s

10 meters in 1 second      v  = 10 m/s 

8 meters in 1 second        v = 8 m/s

5 meters in 1 second        v = 5 m/s

As you can see the total distance is 13 + 9 + 10 + 8 + 5 = 45

and the total time is 1 + 1  + 1 + 1  + 1 = 5  

Challenging speed word problems

Problem #2 : How far is a house in New York if it takes you 5 hours to get there and your average speed is 35 miles per half hour?

First, notice that in the problem we said average speed instead of just speed. It is because you did not just do 35 miles per hour during the entire trip. Your speed changed from times to times, but the average comes to 35 miles per hour.

Second, it is convenient to convert miles per half hour to miles per hour.

35 miles per half hour is 70 miles per hour.

Lastly, convert the formula from speed to distance. 

Now, we have the speed and the time, we can get the distance.

Problem #3 : Your turn!

How far is a house in Florida if it takes you 4 hours to get there and your instantaneous speeds were 70 miles per hour, 50 miles per hour,  60 miles per hour, 10 miles per hour, and 0 miles per hour? 

Take a look also at the speed word problem below

What is speed?

Special Math Topics

Applied math.

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

Average Speed Problems

Related Pages Rate, Time, Distance Solving Speed, Time, Distance Problems Using Algebra More Algebra Lessons

In these lessons, we will learn how to solve word problems involving average speed.

There are three main types of average problems commonly encountered in school algebra: Average (Arithmetic Mean) Weighted Average and Average Speed.

How to calculate Average Speed?

The following diagram shows the formula for average speed. Scroll down the page for more examples and solutions on calculating the average speed.

Examples Of Average Speed Problems

Example: John drove for 3 hours at a rate of 50 miles per hour and for 2 hours at 60 miles per hour. What was his average speed for the whole journey?

Solution: Step 1: The formula for distance is

Distance = Rate × Time Total distance = 50 × 3 + 60 × 2 = 270

Step 2: Total time = 3 + 2 = 5

Step 3: Using the formula:

Answer: The average speed is 54 miles per hour.

Be careful! You will get the wrong answer if you add the two speeds and divide the answer by two.

How To Solve The Average Speed Problem?

How to calculate the average speed?

Example: The speed paradox: If I drive from Oxford to Cambridge at 40 miles per hour and then from Cambridge to Oxford at 60 miles per hour, what is my average speed for the whole journey?

How To Find The Average Speed For A Round Trip?

Example: On Alberto’s drive to his aunt’s house, the traffic was light, and he drove the 45-mile trip in one hour. However, the return trip took his two hours. What was his average trip for the round trip?

How To Find The Average Speed Of An Airplane With Good And Bad Weather?

Example: Mae took a non-stop flight to visit her grandmother. The 750-mile trip took three hours and 45 minutes. Because of the bad weather, the return trip took four hours and 45 minutes. What was her average speed for the round trip?

How To Relate Speed To Distance And Time?

If you are traveling in a car that travels 80km along a road in one hour, we say that you are traveling at an average of 80kn/h.

Average speed is the total distance divided by the total time for the trip. Therefore, speed is distance divided by time.

Instantaneous speed is the speed at which an object is traveling at any particular instant.

If the instantaneous speed of a car remains the same over a period of time, then we say that the car is traveling with constant speed.

The average speed of an object is the same as its instantaneous speed if that object is traveling at a constant speed.

How To Calculate Average Speed In Word Problems?

Example: Keri rollerblades to school, a total distance of 4.5km. She has to slow down twice to cross busy streets, but overall the journey takes her 0.65h. What is Keri’s average speed during the trip?

How To Use Average Speed To Calculate The Distance Traveled?

Example: Elle drives 169 miles from Sheffield to London. Her average speed is 65 mph. She leaves Sheffield at 6:30 a.m. Does she arrive in London by 9:00 a.m.?

How To Use Average Speed To Calculate The Time Taken?

Example: Marie Ann is trying to predict the time required to ride her bike to the nearby beach. She knows that the distance is 45 km and, from other trips, that she can usually average about 20 km/h. Predict how long the trip will take.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Physics Problems with Solutions

• Electric Circuits
• Electrostatic
• Calculators
• Practice Tests
• Simulations
• Velocity and Speed: Problems with Solutions

Problems with detailed solutions on velocity and speed of moving objects.

A man walks 7 km in 2 hours and 2 km in 1 hour in the same direction. a) What is the man's average speed for the whole journey? b) What is the man's average velocity for the whole journey? Solution to Problem 1

A man walks 7 km East in 2 hours and then 2.5 km West in 1 hour. a) What is the man's average speed for the whole journey? b) What is the man's average velocity for the whole journey? Solution to Problem 2

You start walking from a point on a circular field of radius 0.5 km and 1 hour later you are at the same point. a) What is your average speed for the whole journey? b) What is your average velocity for the whole journey? Solution to Problem 3

John drove South 120 km at 60 km/h and then East 150 km at 50 km/h. Determine a) the average speed for the whole journey? b) the magnitude of the average velocity for the whole journey? Solution to Problem 4

If I can walk at an average speed of 5 km/h, how many miles I can walk in two hours? Solution to Problem 5

A train travels along a straight line at a constant speed of 60 mi/h for a distance d and then another distance equal to 2d in the same direction at a constant speed of 80 mi/h. a)What is the average speed of the train for the whole journey? Solution to Problem 6

A car travels 22 km south, 12 km west, and 14 km north in half an hour. a) What is the average speed of the car? b) What is the final displacement of the car? c) What is the average velocity of the car? Solution to Problem 7

More References and links

• Velocity and Speed: Tutorials with Examples
• Acceleration: Tutorials with Examples
• Uniform Acceleration Motion: Problems with Solutions
• Uniform Acceleration Motion: Equations with Explanations

POPULAR PAGES

privacy policy