eratosthenes experiment

Experiment of The Month

A holiday measurement of earth's circumference.

Thanks to Gregor Shapiro for corrections to this article.)

Credit for the first estimate of the Earth's radius goes to Eratosthenes, in Alexandria, around 240 B.C.E. As recounted by Alder (Ken Alder, The Measure of All Things , The Free Press (Simon&Shuster) 2002, p91), Eratosthenes knew of a deep well near Aswan on the Nile where the sun shined all the way to the bottom at noon on the day of the summer solstice. On that day, the sun at noon was directly overhead at Aswan. On the same day, Eratosthenes measured the shadow of the a stick at noon in Alexandria. The length of that shadow was not zero because the sun was not directly overhead in Alexandria.

Eratosthenes analyzed the observations with the assumption that the earth is a sphere and the sun is very far away. The geometry of the situation is sketched at the right. He concluded that the circumference of the earth was about 50 times greater than the distance from Alexandria to Aswan. His results and modern results agree within about 10%.

Because the sun is assumed to be very far away, we believe that the light rays which reach us from the sun are all going in the same direction; they are parallel. (This assertion can be tested by observing a beam of light from the sun which passes through a 1mm hole in a large piece of cardboard.) In the figure, a vertical stick at point A would cast no shadow, a stick at B would cast a "moderate" shadow, and a stick at C would cast a very long shadow.

In Eratosthenes' experiment, A would correspond to the well at Aswan, on the day of the summer equinox, and Alexandria would be located somewhere between A and B.

U.S. Route 95 runs all the way from Maine to Florida. Anyone with access to Route 95 and a tape measure can repeat Eratosthenes' measurement, and can even use a baseline that is longer than his.

Over the winter break, on a trip to Florida from Pennsylvania, the author had the opportunity to repeat these measurements. The measurements were done near the winter solstice, when the sun remains low in the sky for a month or so. The measurements were done over a period of several weeks after the solstice. During that time the sun rises higher in the sky each day, so that the shadow of a vertical stick gets shorter, day by day. Near the solstice, the rate of change of the sun's height is at its minimum, and this effect will be ignored for now.

A tape measure was used for the "vertical stick" and a carpenter's level with an inch scale on top was used to measure the length of the shadow. In the picture above left, the sun light would come from the left and the tape measure would cast its shadow on the level.

In the figure above right, a smaller segment of the spherical earth's surface is shown, with the light rays now shown as dotted lines. Location A represents Florida, and location B represents Pennsylvania. The shadows are represented by heavy lines parallel to the earth's surface. The stick at A is longer, but the short stick at B casts a longer shadow .

The table at the right shows the results. Each entry is for noon on a different day, and the table is ordered with the earliest day at the top. The 17 data points were taken over a period of 24 days. The average shadow angle for Florida has a fairly large standard deviation, partly because measurements were taken at a variety of locations, from Orlando to the Keys. The standard deviation of the Lancaster data must have some other cause.

Taking the averages at face value, we can say that the difference in sun angle between Florida and Pennsylvania is about 10 degrees, with an uncertainty of about 2 degrees. The odometer reading on the car showed 987 miles traveled between the northern edge of Florida and Lancaster, Pennsylvania. The separation of those two locations is smaller, of course, and the average distance to the more southerly Florida locations is larger. We can estimate the separation of the two averages at 1000 miles, with an uncertainty of perhaps 100 miles.

The diagram shows the earth radius which leads to point A and another leading to point B. A little geometry shows that the difference between the shadow angles is the same as the angle between those two radii. In our case, the shadows tell us that we have moved about 10 degrees around the earth when travelling from Florida to Pennsylvania. Since the distance travelled was about 1000 miles, we conclude that the circumference of the earth is about 36,000 miles.

This rough agreement with other measurements of the circumference encourages us to analyze the data more carefully.

The Lancaster measurements show a definite trend, indicated by the solid line. The shadow at Lancaster is getting longer as the year progresses towards spring and the sun rises in the sky. By extending the solid line back in time, we can estimate the shadow angle in Lancaster when we were measuring the shadow in southern Florida. The graph suggests that 15 degrees is a better estimate than 10 degrees for the angle change from Florida to Lancaster.

With 15 degrees corresponding to 1000 miles, we estimate the circumference of the earth at 24,000 miles, in better agreement with published results.

As indicated in the figure, the latitude was measured with a hand-held Global Positioning System receiver. the straight line is a fit to the first 9 measurements, including only the earliest measurement at Lancaster.

The slope of the line should be 1. It is .93, with an uncertainty of .03. The lower than expected slope is probably associated with the shortening shadow, as the days went by. With this caveat, we can say that the agreement between shadow angle and GPS latitude is good.

On the day of the winter solstice, ( a few days before our earliest measurement) the difference between the shadow angle and the GPS latitude is the same as the angle at which the earth's axis is tilted relative to its plane of orbit. The difference between the shadow angle and the GPS latitude is also equal to the intercept of the straight line in the graph. This intercept is 26 degrees with an uncertainty of 1 degree. That result agrees roughly with the official angle of tilt of the earth's axis, 23.5 degrees.

An Alternative Model

A little trigonometry shows that

Using the values 50 degrees and 60 degrees as measured on the trip, with b=1000 miles, we find that h is approximately 2000 miles. This relatively close sun would have been quite plausible to the ancients.

Continuing the calculation, we find that a is approximately 2400 miles and the two distances R1 and R2 are approximately 3000 and 3900 miles, respectively.

That is, as we move from Florida to Pennsylvania, our distance from the sun increases by about 30%. As a consequence, the apparent size of the sun should decrease by 30%. We see no noticeable change in the apparent size of the sun as we make the trip. We conclude that the flat earth/near sun model does not work.

Commercial Lab Band

Commercial ensemble, mbb vs dominican, glorious sounds of the season returns for 19th year, jdogs: the place to be thursday nights, odk inducts new members.

Science in School

The eratosthenes experiment: calculating the earth’s circumference teach article.

Author(s): Sevasti Malamou, Vasileios Kitsakis

On the shoulders of giants: follow in the footsteps of Eratosthenes and measure the circumference of the Earth like he did 2300 years ago.

The following learning scenario is made for secondary school students that are familiar with the concepts of equal angles, from geometry, and tangents, from trigonometry. Moreover, it can also be adjusted for primary school students not familiar with trigonometry: they can make measurements like Eratosthenes did and leave advanced calculations for the teacher.

Brief description

Students can measure the Earth’s circumference like Eratosthenes did approximately 2300 years ago using simple materials and a stick’s shadow made by the Sun. Even though there is a high probability that the measurement will not approximate the true value of the Earth’s circumference, like we know it today, the measuring itself provides a basis for simple mathematical reasoning and scientific thinking.  

Ideally, the experiment should take place on the March or September equinoxes on a sunny, or almost sunny, day. Before starting to measure the Earth’s circumference, students should learn about Eratosthenes, his life, work, and the way he calculated the circumference of the Earth.

Learning objectives

• Describe the geometry of sunlight towards Earth (sunrays are parallel when falling to Earth)
• Understand that equinoxes and solstices are due to the Earth’s movement
• Realize the geographic coordinate system of Earth: latitude and longitude
• Describe how Eratosthenes measured the circumference of the Earth
• Measure angles and distances
• Compare angles and triangles
• Explain measurement errors and suggest ways to minimize them
• Collaborate with other schools on the same longitude

Optional introductory activity: Who was Eratosthenes? Why is his experiment so important nowadays?

Although it seems a simple and easy experiment, it takes time for students to really understand geometry, the direction of the Sun towards Earth on specific days, and the logical sequence of Eratosthenes’ thoughts. 

The goal is not simply to measure the length of the stick and its shadow, but to understand Eratosthenes’ logic behind these simple measurements, and thus, highlight his ingenuity, since almost 2300 years ago he calculated the circumference of the Earth with relatively great accuracy.

We recommend carrying out the introductory activity , so that students understand the importance of Eratosthenes’ experiment, the era during which he did his experiment, what helped him to reach to his conclusions, and the way he managed to accomplish his experiment.

Activity 1: Identify the exact time of the measurement

Before implementing the experiment, which is actually to measure distances and make calculations, we must first determine when the Sun reaches its highest point in the sky on the day of the equinox; what we call local noon (or zenith). This time differs for each school and depends on the school’s position on the globe and should be determined with the best accuracy possible. At this specific time, sunrays fall perpendicularly on the equator, and they are parallel to the equatorial plane, so a vertical bar will have no shadow. On the other hand, in our place at this specific time, a vertical bar will have a shadow.

A calculator tool that can be used is SunCalc . The position and date have to be filled in for the Sun’s culmination time to be calculated. At this exact time on the day of the equinox, students have to measure the stick’s length and its shadow.

This activity only takes a few minutes, but it is also recommended to do the introductory activity to set the context. It should be possible to do the introductory activity and Activities 1 and 2 in one lesson; these should be completed a few days before the measurement lesson on the equinox (Activity 3).

• Internet connection and a suitable device (PC, laptop, tablet, smartphone)

At least 1–2 days before the equinox (when the measurements will be made), you should:

• Explain the experiment (ideally using the introductory activity ).
• Tell your students that many schools are doing this experiment on this specific day.
• Split your class into groups of two students and let them run the web tool SunCalc in the computer lab or use tablets.

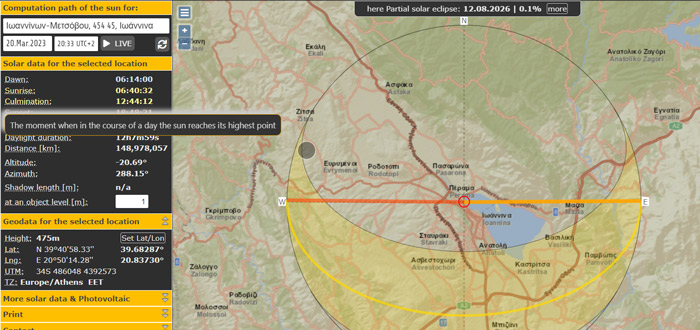
• Find their city/village and school on the map
• Select the required date that the measurements are going to be made (equinoxes are preferred)
• Write down the culmination time

Alternatively, if you don’t have enough time or equipment, you can demonstrate the procedure.

Finding the zenith time for the Sun should only take a few minutes. You can also use the application as a learning object for students and ask them to investigate different sundial characteristics. The tool gives the chance to understand the concept of noon during the year. Students can change the date, and then see the culmination time for each date. Solstices and equinoxes are dates that should be investigated. Local noon is in the midpoint between sunrise and sunset times, and it depends on the latitude and date during the year.

Activity 2: Identify the school’s coordinates

At least one day before the experiment, students should identify the school’s coordinates using online tools. What is to be measured is the distance in kilometres from the schoolyard to the equator along the school’s meridian, which is going to be a curved line, following the Earth’s curvature. All points along this meridian have the same longitude.

Eratosthenes knew the distance between Alexandria and Syene (nowadays Aswan) in stadia (an ancient unit of length). Nowadays, we can measure the distance using electronic applications. You could also get a distance estimate using a real map and a ruler, just like students used to calculate real distances years ago. Especially for younger students, it would be a great chance to refresh their knowledge of map scales. The measurement won’t be as accurate as the one with online tools, but it is a simple estimation.

This activity should only take 10 min.

• Video on how to measure the distance from your school to the equator
• Alternatively, a map and a ruler
• Use a smartphone with a location function.
• Write down the latitude and longitude of the schoolyard.
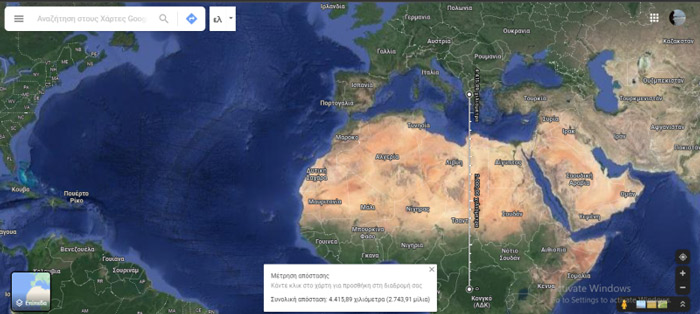
• Measure the distance from your school to the equator. For this step, Google Maps or Google Earth can be used, as shown in the video .
• Write down the distance in kilometres. This information is what students need for their calculations.

Activity 3: Measure like Eratosthenes on the equinox

The day that everyone was expecting has arrived. The teacher has to organize all the required materials before the time that the Sun reaches its highest point. Everything should be prepared in advance because, once the Sun reaches its zenith, there is no time to lose. Students have to act quickly, and they have to know exactly what to do.

• Linear sticks (approximately 1 m long is ideal)
• Right-angle triangles, plumb bobs, carpenter’s levels, or an object that has a right angle to ensure verticality
• Metre sticks or tape measures
• Clock accurate to the minute (or a smartphone)

Student worksheet

• To measure the length of the sticks when the Sun is overhead, supply students with the necessary materials and worksheet a short time before the measurement time.
• Go with your students into the schoolyard at least 10–15 min before the zenith time for your latitude.
• Split the class into groups of four.
• Ask each member of the group to take on a specific role. Student 1 will be responsible for the time, student 2 will act as a scribe and record the measurements, and students 3 and 4 will do the measurements.
• Make sure that each group has a set of materials (a linear stick, a metre stick, a right-angle triangle, a pencil, a clock, and a worksheet).
• Ask students to measure the length of the stick before the zenith time and write their measurements on the worksheet.
• About 2–3 min before the zenith time, ask students to place and hold the sticks vertically.
• Use the right-angle triangle to make sure that the sticks are vertical. Check that all groups achieve verticality.
• When the Sun reaches its highest point in the sky, ask students to measure the stick’s shadow on the ground and write its value on the worksheet.
• If students don’t manage to measure the stick’s length before the zenith time, or if they want to be sure about it, they can measure it again after the local noon time.

After measuring the two lengths (stick length and shadow length) and writing the values on the worksheet, data processing begins. Calculations can be done in the schoolyard, with students working in groups and comparing their results with their classmates. Alternatively, if there is a lack of time, calculations can be done in the classroom at another time. Students can use scientific calculators (or the one on their smartphones) to calculate the angle θ .

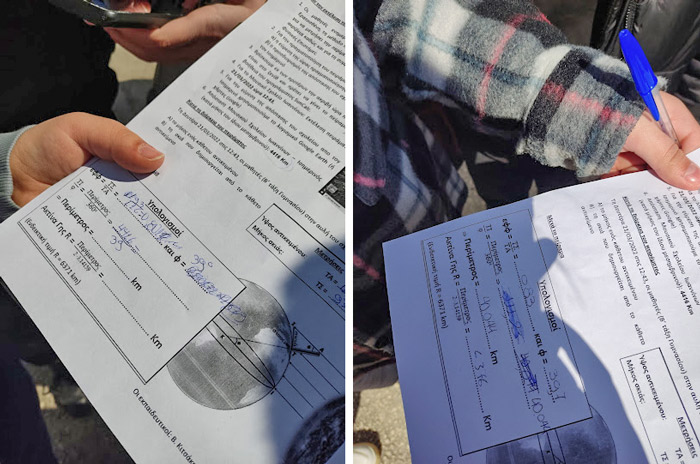
Extension activities

There are several extension activities that can be done to make the learning experience more meaningful, such as calculating the radius of the Earth and collaborating with another school. These are described fully in the supporting material.

When doing the calculations and exporting the results, you could use the following questions as the basis for a discussion:

• What could be the measurement errors during the experiment?
• What can be done to minimize errors?
• What errors could have been made by Eratosthenes when he performed his own experiment 2300 years ago? To answer this, the globe could be used, with pins on Alexandria and Syene. Alternatively, students can observe the two cities on Google Earth.
• Angle θ , calculated during the experiment, also represents what?
• If you do the experiment during the summer/winter solstice, what would you change? Explain.
• Why did Eratosthenes make his measurements during the summer solstice? Could he do it on the spring or autumn equinoxes? Explain.

As a conclusion, you can emphasize to your students that science often develops from a simple idea and an inquisitive mind.

[1] Panhellenic Union of Heads of Laboratory Centers of Natural Sciences (Greek language): https://panekfe.gr/eratosthenes/

• Find more teaching resources relating to the Eratosthenes experiment on the eu website.
• Read more about the life and work of Eratosthenes of Cyrene .
• Watch a video about Eratosthenes by Carl Sagan.
• Explore data visualization by sketching graphs from story videos of everyday events: Reuterswärd E (2022) Graphing stories . Science in School 58 .
• Discover how physicists study very small and large objects that cannot be directly observed or measured: Akhobadze K (2021) Exploring the universe: from very small to very large . Science in School 55.
• Get your students to use their smartphones for some hands-on astronomy: Rath G, Jeanjacquot P, Hayes E (2016) Smart measurements of the heavens . Science in School 36: 37–42.
• Challenge your students to solve the mystery box puzzle while learning about the nature of science: Kranjc Horvat A (2022) The mystery box challenge: explore the nature of science .  Science in School 59 .
• Measure distances to the stars like real astronomers with this classroom activity: Pössel M (2017) Finding the scale of space . Science in School 40 : 40–45.
• Measure the distance between Earth and the Moon with the help of radio signals: Middelkoop R (2017) To the Moon and back: reflecting a radio signal to calculate the distance . Science in School 41: 44–48.

Sevasti Malamou is a secondary school physics teacher at the Music School of Ioannina Nikolaos Doumpas, Greece. She has also taught chemistry, biology, and geography and enjoys using innovative methods to teach science. She holds master’s degrees in both electronics and telecommunications, and physics didactics.

Vasilios Kitsakis is a secondary school maths teacher and currently headmaster at the Music School of Ioannina Nikolaos Doumpas, Greece. He holds master’s degrees in studies in education and educational management. He has taken part in training programs and conferences as a speaker.

This article introduces ideas and activities that move teachers and students from a historical concept to its replication using modern technologies.

Marie Walsh, Science Lecturer, Ireland

Supporting materials

Introductory activity

Download this article as a PDF

Share this article

Subscribe to our newsletter, related articles.

Smart measurements of the heavens

Get your students to use their smartphones for some hands-on…

The mystery box challenge: explore the nature of science

Thinking outside the box: explore the nature of science by building LEGO mystery boxes and challenging your students to solve the…

Exploring the universe: from very small to very large

How do physicists study very small objects (like molecules, atoms, and subatomic particles) and very large objects (such as galaxies) that cannot be…

Before we begin a few definitions:

Tropic of Cancer - is one of five major circles of latitude that mark maps of the Earth. The Tropic of Cancer currently latitude is 23° 26′ 22″ north of the Equator.

Local noon is when the sun is the highest in the sky and can be quite different from 12:00 noon on the clock.

Solstice - is an astronomical event that happens twice each year, when the tilt of the Earth's axis is most inclined toward or away from the Sun. In the northern hemisphere, the maximum inclination toward the sun is around 21 June (the summer solstice) and with the maximum inclination away around 21 December (the winter solstice). For the southern hemisphere winter and summer solstices are exchanged.

What matters for our experiment is the fact that on the summer solstice, local noon, the sun rays are just overhead (at a right angle to the ground) on the Tropic of Cancer.

Repeat Eratosthenes' Experiment

Eratosthenes measured, at his local noon in Alexandria, the angle of elevation of the sun on the summer solstice (21 June). Eratosthenes used the local noon and no other time of the day since at local noon all relevant places and sunrays are placed on the same imaginary plane enabling the use of simple geometry for his calculations. In order to repeat Eratosthenes’ experiment you’ll have to do the same.

First, calculate your local noon because it may be quite different from 12:00 noon on the clock. There are several ways to compute its exact occurrence. Basically, local noon is half-way between sunrise and sunset. You can obtain sunrise and sunset times, for June 21, from your local paper or from this link: http://aa.usno.navy.mil... which also calculates local noon (sun transit). You can also obtain it by yourself by using a sundial or find out when the shadow is the shortest around noon time.

On June 21 erect a vertical straight stick or pole of about 1 meter using a carpenter’s level and measure the length of the shadow it casts at your local noon. With simple trigonometry you can obtain the angle of the elevation of the sun. You can also obtain the angle, without trigonometry, by drawing the stick and shadow proportionally and measuring it with a protractor. You can compare your results with a web based applet like this: http://www.jgiesen.de/azimuth but be careful to use it correctly (insert your correct time zone, local noon, coordinates, date and ensure that the dropdown menu points to elevation).

After you get the angle of sun elevation, it’s very easy to calculate the zenith angle by subtracting it from 90°, like Eratosthenes did. Now you’ll have to measure the distance from your location to the Tropic of Cancer latitude line - not by camel caravans of course, the Eratosthenes way. You can use a relatively large scale map, but take in account that maps tend to distort distance and the best option is to use a globe. The distance from your location to the Tropic of Cancer should be measured from north to south. In other words the distance line has to cut the Tropic of Cancer at a right angle. There are also web based calculators for this: https://web.archive.org... .

Now it's easy to calculate the Earth circumference by using the following formula:

Likewise, you can also perform this experiment on the winter solstice that takes place around 21 December, but you’ll have to measure your distance from the Tropic of Capricorn instead from the Tropic of Cancer because on this date the sun reaches its highest degree of elevation on the Tropic of Capricorn (23° 26′ 22″ south of the Equator).

It is also possible to perform this experiment on the two Equinoxes which occur on 20 March and 23 September each year when the sun is crossing the equator at the local noon on those dates and the sun rays are just overhead the equator at a right angle to the ground. But instead to measure your distance from the Tropic of Cancer or the Tropic of Capricorn you’ll have to measure it from the equator.

There is another option and you can perform this experiment on any other date of the year, at local noon time, but you should have some partner located on your longitude willing to measure sun elevation at the same time. Take in account that you'll have to be a little careful treating correctly the sun angles obtained in this case.

At any date the sun reaches its highest position, at noon time, at some latitude. From here is clear that if the two places involved are located on the same side of this latitude (north or south) the shadows will be casted at the same direction and the obtained angles should be subtracted from each other, whereas if the places are located on different sides of this latitude the shadows will be casted at different directions (southward or northward) and the angles should be added up.

Further Reading

Measuring the World: Eratosthenes and the Earth’s Circumference

Share The History!

Eratosthenes, an ancient Greek astronomer, mathematician, and geographer, is widely known for his remarkable achievement in calculating the circumference of the Earth.

Eratosthenes was born in Cyrene, a Greek colony in modern-day Libya, in 276 BCE. He later moved to Alexandria, where he became the chief librarian at the Library of Alexandria, one of the most significant libraries of the ancient world.

Eratosthenes’ method of measuring the Earth’s circumference was revolutionary for his time.

He noticed that on the summer solstice, the sun was directly overhead in Syene, a city located on the Tropic of Cancer, while it was at an angle in Alexandria.

He reasoned that if the Earth was flat, the angle of the sun’s rays would be the same in both cities. However, since the Earth is round, the angle of the sun’s rays would be different.

By measuring the angle of the sun’s rays in Alexandria and knowing the distance between Alexandria and Syene, Eratosthenes was able to calculate the Earth’s circumference with remarkable accuracy.

Eratosthenes’ accomplishment in measuring the Earth’s circumference was not only a significant achievement in the field of astronomy but also in the history of science.

His method of measuring the Earth’s circumference was a crucial step in understanding the shape and size of the Earth, which later paved the way for other significant discoveries in the field of geography and cartography.

The Life of Eratosthenes

Eratosthenes was a Greek astronomer, geographer, mathematician, and poet who lived from 276-195 BCE.

He was born in Cyrene, a Greek colony in Libya, and later moved to Alexandria, where he spent most of his life.

Eratosthenes was educated in Athens and studied under some of the most prominent scholars of his time.

He moved to Alexandria, where he became the head of the Library at Alexandria, one of the greatest libraries of the ancient world.

Eratosthenes was a polymath who made significant contributions to many fields, including mathematics, geography, and astronomy.

Contributions to Mathematics and Geography

Eratosthenes is best known for his work in geography and for being the first person to calculate the circumference of the Earth.

He used his knowledge of geometry and trigonometry to measure the angle of the sun’s rays at two different locations in Egypt.

By using the difference in angle, he was able to calculate the circumference of the Earth with remarkable accuracy.

Eratosthenes also made significant contributions to mathematics.

He developed the Sieve of Eratosthenes, a method for identifying prime numbers.

This method involves creating a list of numbers and crossing out all the multiples of each prime number until only prime numbers remain.The Sieve of Eratosthenes is still used today to find prime numbers.

Eratosthenes’ work on prime numbers was groundbreaking.He realized that prime numbers are the building blocks of all other numbers and that they play a crucial role in mathematics.

Measuring the Earth’s Circumference – The Experiment at Syene and Alexandria

Eratosthenes’ method was relatively simple.

He first measured the angle of the sun at the summer solstice in Syene, a city located in southern Egypt.

In Syene, the sun was directly overhead, so a vertical stick cast no shadow.

Eratosthenes then measured the angle of the sun in Alexandria, a city located north of Syene. In Alexandria, a vertical stick cast a shadow.

By observing the difference between the angles, Eratosthenes was able to calculate the angle between the two cities and the distance between them.

Calculating the Circumference

Eratosthenes knew that the distance between Syene and Alexandria was approximately 5,000 stadia, a unit of length used in ancient Greece.

He also knew the approximate size of a degree of latitude, which is about 111 kilometers or 69 miles.

By dividing the distance between Syene and Alexandria by the size of a degree, Eratosthenes was able to calculate the angle between the two cities, which he found to be 7.2 degrees.

Eratosthenes then used this angle to calculate the Earth’s circumference.

He knew that 7.2 degrees was 1/50th of a circle (360 degrees), so he multiplied the distance between Syene and Alexandria by 50 to get the Earth’s circumference.

Eratosthenes’ value for the Earth’s circumference was approximately 39,375 kilometers or 24,662 miles, which is remarkably close to the modern value of 40,075 kilometers or 24,901 miles.

The Importance of Eratosthenes’ Measurement

Eratosthenes’ measurement of the Earth’s circumference was a significant achievement in the history of science and learning.

It was the first time that anyone had accurately measured the Earth’s size, and it had important implications for navigation, geodesy, and modern geography.

Eratosthenes’ method also demonstrated the power of mathematics and geometry to solve complex scientific problems.

The Legacy of Eratosthenes

Eratosthenes’ groundbreaking work in calculating the Earth’s circumference had a profound impact on later scholars and geographers.

His algorithm for measuring the Earth’s size and his contributions to the field of geography were studied and built upon by many Greek scholars, including Hipparchus, Posidonius, and Strabo.

Aristotle, who was one of the most influential philosophers of his time, was also impressed by Eratosthenes’ work and recognized its significance.

Eratosthenes’ method was used by Ptolemy, who created the Almagest, a comprehensive treatise on astronomy that was used as a standard reference for centuries.

Eratosthenes’ work also had practical applications.

Christopher Columbus, for example, used Eratosthenes’ calculations to estimate the distance of his voyage to the New World.

Eratosthenes’ algorithm was also used to measure the diameter of the Moon and to determine the longitude of different locations on Earth.

Eratosthenes’ Work in the Context of Modern Science

Eratosthenes’ work was groundbreaking not just because of the accuracy of his measurements, but also because of the scientific method he used to arrive at his calculations.

His approach to measuring the Earth’s circumference was based on empirical evidence and mathematical reasoning. His algorithm was a major step forward in the development of scientific methodology.

Eratosthenes’ work also had a significant impact on the development of chronology and the study of history. His chronographies, which were lists of events arranged in chronological order, were used to create a timeline of ancient history.

He also studied the axial tilt of the Earth and the Tropic of Cancer. His work on lunar eclipses helped to refine the accuracy of calendars.

Despite being blind for most of his life, Eratosthenes made significant contributions to the fields of mathematics, astronomy, and geography.

His work set a high standard for academic excellence. His scale of the Earth, which he developed through his project to measure the Earth’s circumference, was a remarkable achievement that continues to inspire scientists and scholars today.

You may also like

The Battle of Thermopylae – The 300 Spartans’ Heroic Stand

Hippolyta and the Amazons – The Mythical Warrior Women of Ancient Greece

Penelope – The Faithful Wife Whose Loyalty Helped Shape the Odyssey

Add comment, cancel reply.

Save my name, email, and website in this browser for the next time I comment.

• Ancient Egypt 11
• Ancient Greece 9
• Ancient Rome 11
• Anglo-Saxons 4
• Byzantines 3
• Medieval History 69
• Vikings 178

Dido of Carthage – The Queen Whose Affair With Aeneas Influenced the Founding of Rome

Antigone – The Princess Whose Defiance and Beauty Led to a Tragic Conflict

This measurement is more than 2,200 years old, and its accuracy is remarkable

Topic: Mathematics Education

Ancient mathematicians used their knowledge of geometry to take accurate measurements of earth ( Getty: Aris Messinis )

There are so many negative numbers and statistics flying around at the moment, it's a little overwhelming.

So let me tell you an inspiring story about numbers: it will be a relief to think about something else for a few minutes.

Travel back in time

About 2,250 years ago, there was a man called Eratosthenes.

He was one of those ancient Greeks who changed the world.

He was a polymath, someone with expert knowledge of a range of topics.

A mathematician, geographer, astronomer, philosopher, poet, and music theorist. 

He's famous for being the first person known to have measured the earth's circumference.

How did he do it?

It's surprisingly simple. You just need some basic geometry.

Watch the short clip below of the great Carl Sagan to see how it was done. 

I've set it to play from the 4 min 11 sec mark, because that's where Sagan explains the calculations. But the few minutes before that point are also wonderful.

In case you couldn't watch or hear the video, I'll explain the story quickly.

Around 245 BC, when Eratosthenes was in his 30s, he was working as a librarian in the famous Library of Alexandria in Egypt.

It was there where he read about a water well in the city of Syene (modern-day Aswan in southern Egypt).

At midday every summer solstice, the sun would shine directly down into the well, illuminating the water at the bottom - but casting no shadow on the walls of the well.

It meant the sun sat directly above Syene at that exact moment.

So Eratosthenes wondered, if he stuck a pole in the ground in Alexandria at that same moment, would it cast a shadow?

And it turns out it did.

What did it prove?

His little experiment demonstrated that the surface of the earth was curved like a sphere.

Why? Because his pole in Alexandria was sticking straight into the air but the curvature of the earth made it face slightly away from the sun, causing the pole to throw a small shadow onto the ground.

And that allowed him to do something else.

Since he knew the height of the pole, and the length of the shadow it cast, it meant he knew the lengths of two sides of a right-angled triangle.

That meant he could figure out the length of the third side of the triangle, and he could also figure out the angle at the top of the pole, between the sunbeam and the pole itself.

It was 7.2 degrees.

Therefore, he knew the sun was hitting Alexandria at an angle of 7.2 degrees precisely at midday on the summer solstice.

When a fraction goes a long way

And that left him with one final measurement.

To figure out the circumference of the earth, he needed to somehow measure the distance between Alexandria and Syene.

So he asked someone (or a team of people) to walk it.

Those people were called "bematists", professional surveyors who were trained to measure vast distances extremely accurately by pacing the distance.

They estimated the distance between the two cities was roughly 5,000 stadia (or 800 kilometres).

And that was everything Eratosthenes needed.

He had all the ingredients to calculate the circumference of the earth.

A few assumptions help

Let's go.

Assume the earth is a perfect sphere (it's not, but it's not a problem for these calculations).

We know there are 360 degrees in a circle.

If you cut the earth in half, the earth's great circle will obviously have 360 degrees, and the circumference of that circle (i.e. the total length of its perimeter) could be divided up into equal bits of whatever length.

Eratosthenes knew that the distance between Syene and Alexandria was 7.2 degrees along the surface of the earth.

So how many of those distances would he need to stretch around the entire 360 degree circumference of the earth?

He divided 360 by 7.2, which gave a neat 50.

That meant, given the distance between Alexandria and Syene was 800 kilometres, all he had to do was multiply 800 by 50, which came to 40,000.

And that was it.

The circumference of the earth was 40,000 kilometres, according to Eratosthenes' calculations.

The bematists estimated that Syene was 5,000 stadia (or 800 kilometres) away from Alexandria, which gave Eratosthenes the final number he needed to work out the earth's circumference ( Source: Khan Academy, "Eratosthenes of Cyrene: Measuring the Circumference of the Earth."  )

Was he correct?

He was incredibly close.

As it turns out, the meridional circumference of Earth (from pole to pole) is roughly 40,008 km, and the equatorial circumference is about 40,075 km (it's bigger at the equator because Earth slightly bulges in its middle).

Not bad for someone with such rudimentary tools.

Eratosthenes used his new knowledge to revolutionise map making.

He drew a map of the known world with parallels and meridians, making it possible to estimate real distances between objects, and plotted the names and locations of hundreds of cities over the grid.

It was the beginning of modern geography.

Anyway, I hope that's been a pleasant escape from reality.

When so much attention is focused on the maths of hospitalisations and vaccinations and contagion, it's easy to forget that maths can also be a source of innocent joy.

Take care this week.

Discovering the size of the Earth: The Eratosthenes experiment

by Angelos Alexopoulos | 15/03/2023 | Blog

Get ready to take your students on a journey back in time to the ancient world of Greece, where a brilliant scholar made a groundbreaking discovery that would change the course of history forever.

In 240 BC, Eratosthenes of Cyrene, a Greek polymath and chief librarian at the Library of Alexandria, accomplished what no one before him had been able to do – he measured the circumference of the Earth! This remarkable feat was achieved through an inquiry-based activity that involved keen observation, critical thinking, and precise calculations. Back then, the ancient Greeks knew that the Earth was round, but they had no idea about its size. Eratosthenes’ ingenious experiment involved observing the sun’s angle at noon on the summer solstice in two different cities – Syene and Alexandria – which were located at the same longitude. He noticed that at noon on the summer solstice, the sun was directly overhead of a well in Syene, without casting any shadows, while in Alexandria, a stick cast a shadow at the same time, making an angle of about 7.2 degrees. Using this information and the distance between the two cities, Eratosthenes was able to calculate the Earth’s circumference with an impressive degree of accuracy, within 15% of today’s measured values. This milestone discovery not only proved that the Earth was much larger than previously thought but also paved the way for future scientific discoveries.

Fast forward 2250 years and Eratosthenes’ experiment remains one of the most beautiful and insightful experiments in the history of science. It is also an exemplary inquiry-based activity that can help introduce students to the scientific way of thinking. By recreating Eratosthenes’ experiment in the classroom, students can learn about the power of observation, critical thinking, and mathematical reasoning.

Carl Sagan explains…

Watch this video where Carl Sagan explains this monumental experiment.

Want to take your students on an exciting journey through time and space, and inspire the next generation of scientists and researchers with the Eratosthenes Experiment? Take part in the international photo contest led by Ellinogermaniki Agogi. Hurry up!   The deadline for submitting your photo is 10 April 2023 .