
Statistics Made Easy

The Complete Guide: Hypothesis Testing in R
A hypothesis test is a formal statistical test we use to reject or fail to reject some statistical hypothesis.
This tutorial explains how to perform the following hypothesis tests in R:
- One sample t-test
- Two sample t-test
- Paired samples t-test
We can use the t.test() function in R to perform each type of test:
- x, y: The two samples of data.
- alternative: The alternative hypothesis of the test.
- mu: The true value of the mean.
- paired: Whether to perform a paired t-test or not.
- var.equal: Whether to assume the variances are equal between the samples.
- conf.level: The confidence level to use.
The following examples show how to use this function in practice.
Example 1: One Sample t-test in R
A one sample t-test is used to test whether or not the mean of a population is equal to some value.
For example, suppose we want to know whether or not the mean weight of a certain species of some turtle is equal to 310 pounds. We go out and collect a simple random sample of turtles with the following weights:
Weights : 300, 315, 320, 311, 314, 309, 300, 308, 305, 303, 305, 301, 303
The following code shows how to perform this one sample t-test in R:
From the output we can see:
- t-test statistic: -1.5848
- degrees of freedom: 12
- p-value: 0.139
- 95% confidence interval for true mean: [303.4236, 311.0379]
- mean of turtle weights: 307.230
Since the p-value of the test (0.139) is not less than .05, we fail to reject the null hypothesis.
This means we do not have sufficient evidence to say that the mean weight of this species of turtle is different from 310 pounds.
Example 2: Two Sample t-test in R
A two sample t-test is used to test whether or not the means of two populations are equal.
For example, suppose we want to know whether or not the mean weight between two different species of turtles is equal. To test this, we collect a simple random sample of turtles from each species with the following weights:
Sample 1 : 300, 315, 320, 311, 314, 309, 300, 308, 305, 303, 305, 301, 303
Sample 2 : 335, 329, 322, 321, 324, 319, 304, 308, 305, 311, 307, 300, 305
The following code shows how to perform this two sample t-test in R:
- t-test statistic: -2.1009
- degrees of freedom: 19.112
- p-value: 0.04914
- 95% confidence interval for true mean difference: [-14.74, -0.03]
- mean of sample 1 weights: 307.2308
- mean of sample 2 weights: 314.6154
Since the p-value of the test (0.04914) is less than .05, we reject the null hypothesis.
This means we have sufficient evidence to say that the mean weight between the two species is not equal.
Example 3: Paired Samples t-test in R
A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.
For example, suppose we want to know whether or not a certain training program is able to increase the max vertical jump (in inches) of basketball players.
To test this, we may recruit a simple random sample of 12 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month.
The following data shows the max jump height (in inches) before and after using the training program for each player:
Before : 22, 24, 20, 19, 19, 20, 22, 25, 24, 23, 22, 21
After : 23, 25, 20, 24, 18, 22, 23, 28, 24, 25, 24, 20
The following code shows how to perform this paired samples t-test in R:
- t-test statistic: -2.5289
- degrees of freedom: 11
- p-value: 0.02803
- 95% confidence interval for true mean difference: [-2.34, -0.16]
- mean difference between before and after: -1.25
Since the p-value of the test (0.02803) is less than .05, we reject the null hypothesis.
This means we have sufficient evidence to say that the mean jump height before and after using the training program is not equal.
Additional Resources
Use the following online calculators to automatically perform various t-tests:
One Sample t-test Calculator Two Sample t-test Calculator Paired Samples t-test Calculator
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.
Linear Hypothesis Tests
Most regression output will include the results of frequentist hypothesis tests comparing each coefficient to 0. However, in many cases, you may be interested in whether a linear sum of the coefficients is 0. For example, in the regression
You may be interested to see if \(GoodThing\) and \(BadThing\) (both binary variables) cancel each other out. So you would want to do a test of \(\beta_1 - \beta_2 = 0\).
Alternately, you may want to do a joint significance test of multiple linear hypotheses. For example, you may be interested in whether \(\beta_1\) or \(\beta_2\) are nonzero and so would want to jointly test the hypotheses \(\beta_1 = 0\) and \(\beta_2=0\) rather than doing them one at a time. Note the and here, since if either one or the other is rejected, we reject the null.
Keep in Mind
- Be sure to carefully interpret the result. If you are doing a joint test, rejection means that at least one of your hypotheses can be rejected, not each of them. And you don’t necessarily know which ones can be rejected!
- Generally, linear hypothesis tests are performed using F-statistics. However, there are alternate approaches such as likelihood tests or chi-squared tests. Be sure you know which on you’re getting.
- Conceptually, what is going on with linear hypothesis tests is that they compare the model you’ve estimated against a more restrictive one that requires your restrictions (hypotheses) to be true. If the test you have in mind is too complex for the software to figure out on its own, you might be able to do it on your own by taking the sum of squared residuals in your original unrestricted model (\(SSR_{UR}\)), estimate the alternate model with the restriction in place (\(SSR_R\)) and then calculate the F-statistic for the joint test using \(F_{q,n-k-1} = ((SSR_R - SSR_{UR})/q)/(SSR_{UR}/(n-k-1))\).
Also Consider
- The process for testing a nonlinear combination of your coefficients, for example testing if \(\beta_1\times\beta_2 = 1\) or \(\sqrt{\beta_1} = .5\), is generally different. See Nonlinear hypothesis tests .
Implementations
Linear hypothesis test in R can be performed for most regression models using the linearHypothesis() function in the car package. See this guide for more information.
Tests of coefficients in Stata can generally be performed using the built-in test command.
Hypothesis Tests in R
This tutorial covers basic hypothesis testing in R.
- Normality tests
- Shapiro-Wilk normality test
- Kolmogorov-Smirnov test
- Comparing central tendencies: Tests with continuous / discrete data
- One-sample t-test : Normally-distributed sample vs. expected mean
- Two-sample t-test : Two normally-distributed samples
- Wilcoxen rank sum : Two non-normally-distributed samples
- Weighted two-sample t-test : Two continuous samples with weights
- Comparing proportions: Tests with categorical data
- Chi-squared goodness of fit test : Sampled frequencies of categorical values vs. expected frequencies
- Chi-squared independence test : Two sampled frequencies of categorical values
- Weighted chi-squared independence test : Two weighted sampled frequencies of categorical values
- Comparing multiple groups: Tests with categorical and continuous / discrete data
- Analysis of Variation (ANOVA) : Normally-distributed samples in groups defined by categorical variable(s)
- Kruskal-Wallace One-Way Analysis of Variance : Nonparametric test of the significance of differences between two or more groups
Hypothesis Testing
Science is "knowledge or a system of knowledge covering general truths or the operation of general laws especially as obtained and tested through scientific method" (Merriam-Webster 2022) .
The idealized world of the scientific method is question-driven , with the collection and analysis of data determined by the formulation of research questions and the testing of hypotheses. Hypotheses are tentative assumptions about what the answers to your research questions may be.
- Formulate questions: How can I understand some phenomenon?
- Literature review: What does existing research say about my questions?
- Formulate hypotheses: What do I think the answers to my questions will be?
- Collect data: What data can I gather to test my hypothesis?
- Test hypotheses: Does the data support my hypothesis?
- Communicate results: Who else needs to know about this?
- Formulate questions: Frame missing knowledge about a phenomenon as research question(s).
- Literature review: A literature review is an investigation of what existing research says about the phenomenon you are studying. A thorough literature review is essential to identify gaps in existing knowledge you can fill, and to avoid unnecessarily duplicating existing research.
- Formulate hypotheses: Develop possible answers to your research questions.
- Collect data: Acquire data that supports or refutes the hypothesis.
- Test hypotheses: Run tools to determine if the data corroborates the hypothesis.
- Communicate results: Share your findings with the broader community that might find them useful.
While the process of knowledge production is, in practice, often more iterative than this waterfall model, the testing of hypotheses is usually a fundamental element of scientific endeavors involving quantitative data.

The Problem of Induction
The scientific method looks to the past or present to build a model that can be used to infer what will happen in the future. General knowledge asserts that given a particular set of conditions, a particular outcome will or is likely to occur.
The problem of induction is that we cannot be 100% certain that what we are assuming is a general principle is not, in fact, specific to the particular set of conditions when we made our empirical observations. We cannot prove that that such principles will hold true under future conditions or different locations that we have not yet experienced (Vickers 2014) .
The problem of induction is often associated with the 18th-century British philosopher David Hume . This problem is especially vexing in the study of human beings, where behaviors are a function of complex social interactions that vary over both space and time.

Falsification
One way of addressing the problem of induction was proposed by the 20th-century Viennese philosopher Karl Popper .
Rather than try to prove a hypothesis is true, which we cannot do because we cannot know all possible situations that will arise in the future, we should instead concentrate on falsification , where we try to find situations where a hypothesis is false. While you cannot prove your hypothesis will always be true, you only need to find one situation where the hypothesis is false to demonstrate that the hypothesis can be false (Popper 1962) .
If a hypothesis is not demonstrated to be false by a particular test, we have corroborated that hypothesis. While corroboration does not "prove" anything with 100% certainty, by subjecting a hypothesis to multiple tests that fail to demonstrate that it is false, we can have increasing confidence that our hypothesis reflects reality.

Null and Alternative Hypotheses
In scientific inquiry, we are often concerned with whether a factor we are considering (such as taking a specific drug) results in a specific effect (such as reduced recovery time).
To evaluate whether a factor results in an effect, we will perform an experiment and / or gather data. For example, in a clinical drug trial, half of the test subjects will be given the drug, and half will be given a placebo (something that appears to be the drug but is actually a neutral substance).

Because the data we gather will usually only be a portion (sample) of total possible people or places that could be affected (population), there is a possibility that the sample is unrepresentative of the population. We use a statistical test that considers that uncertainty when assessing whether an effect is associated with a factor.
- Statistical testing begins with an alternative hypothesis (H 1 ) that states that the factor we are considering results in a particular effect. The alternative hypothesis is based on the research question and the type of statistical test being used.
- Because of the problem of induction , we cannot prove our alternative hypothesis. However, under the concept of falsification , we can evaluate the data to see if there is a significant probability that our data falsifies our alternative hypothesis (Wilkinson 2012) .
- The null hypothesis (H 0 ) states that the factor has no effect. The null hypothesis is the opposite of the alternative hypothesis. The null hypothesis is what we are testing when we perform a hypothesis test.

The output of a statistical test like the t-test is a p -value. A p -value is the probability that any effects we see in the sampled data are the result of random sampling error (chance).
- If a p -value is greater than the significance level (0.05 for 5% significance) we fail to reject the null hypothesis since there is a significant possibility that our results falsify our alternative hypothesis.
- If a p -value is lower than the significance level (0.05 for 5% significance) we reject the null hypothesis and have corroborated (provided evidence for) our alternative hypothesis.
The calculation and interpretation of the p -value goes back to the central limit theorem , which states that random sampling error has a normal distribution.

Using our example of a clinical drug trial, if the mean recovery times for the two groups are close enough together that there is a significant possibility ( p > 0.05) that the recovery times are the same (falsification), we fail to reject the null hypothesis.

However, if the mean recovery times for the two groups are far enough apart that the probability they are the same is under the level of significance ( p < 0.05), we reject the null hypothesis and have corroborated our alternative hypothesis.

Significance means that an effect is "probably caused by something other than mere chance" (Merriam-Webster 2022) .
- The significance level (α) is the threshold for significance and, by convention, is usually 5%, 10%, or 1%, which corresponds to 95% confidence, 90% confidence, or 99% confidence, respectively.
- A factor is considered statistically significant if the probability that the effect we see in the data is a result of random sampling error (the p -value) is below the chosen significance level.
- A statistical test is used to evaluate whether a factor being considered is statistically significant (Gallo 2016) .
Type I vs. Type II Errors
Although we are making a binary choice between rejecting and failing to reject the null hypothesis, because we are using sampled data, there is always the possibility that the choice we have made is an error.
There are two types of errors that can occur in hypothesis testing.
- Type I error (false positive) occurs when a low p -value causes us to reject the null hypothesis, but the factor does not actually result in the effect.
- Type II error (false negative) occurs when a high p -value causes us to fail to reject the null hypothesis, but the factor does actually result in the effect.
The numbering of the errors reflects the predisposition of the scientific method to be fundamentally skeptical . Accepting a fact about the world as true when it is not true is considered worse than rejecting a fact about the world that actually is true.

Statistical Significance vs. Importance
When we fail to reject the null hypothesis, we have found information that is commonly called statistically significant . But there are multiple challenges with this terminology.
First, statistical significance is distinct from importance (NIST 2012) . For example, if sampled data reveals a statistically significant difference in cancer rates, that does not mean that the increased risk is important enough to justify expensive mitigation measures. All statistical results require critical interpretation within the context of the phenomenon being observed. People with different values and incentives can have different interpretations of whether statistically significant results are important.
Second, the use of 95% probability for defining confidence intervals is an arbitrary convention. This creates a good vs. bad binary that suggests a "finality and certitude that are rarely justified." Alternative approaches like Beyesian statistics that express results as probabilities can offer more nuanced ways of dealing with complexity and uncertainty (Clayton 2022) .
Science vs. Non-science
Not all ideas can be falsified, and Popper uses the distinction between falsifiable and non-falsifiable ideas to make a distinction between science and non-science. In order for an idea to be science it must be an idea that can be demonstrated to be false.
While Popper asserts there is still value in ideas that are not falsifiable, such ideas are not science in his conception of what science is. Such non-science ideas often involve questions of subjective values or unseen forces that are complex, amorphous, or difficult to objectively observe.
| Falsifiable (Science) | Non-Falsifiable (Non-Science) |
|---|---|
| Murder death rates by firearms tend to be higher in countries with higher gun ownership rates | Murder is wrong |
| Marijuana users may be more likely than nonusers to | The benefits of marijuana outweigh the risks |
| Job candidates who meaningfully research the companies they are interviewing with have higher success rates | Prayer improves success in job interviews |
Example Data
As example data, this tutorial will use a table of anonymized individual responses from the CDC's Behavioral Risk Factor Surveillance System . The BRFSS is a "system of health-related telephone surveys that collect state data about U.S. residents regarding their health-related risk behaviors, chronic health conditions, and use of preventive services" (CDC 2019) .
A CSV file with the selected variables used in this tutorial is available here and can be imported into R with read.csv() .
Guidance on how to download and process this data directly from the CDC website is available here...
Variable Types
The publicly-available BRFSS data contains a wide variety of discrete, ordinal, and categorical variables. Variables often contain special codes for non-responsiveness or missing (NA) values. Examples of how to clean these variables are given here...
The BRFSS has a codebook that gives the survey questions associated with each variable, and the way that responses are encoded in the variable values.

Normality Tests
Tests are commonly divided into two groups depending on whether they are built on the assumption that the continuous variable has a normal distribution.
- Parametric tests presume a normal distribution.
- Non-parametric tests can work with normal and non-normal distributions.
The distinction between parametric and non-parametric techniques is especially important when working with small numbers of samples (less than 40 or so) from a larger population.
The normality tests given below do not work with large numbers of values, but with many statistical techniques, violations of normality assumptions do not cause major problems when large sample sizes are used. (Ghasemi and Sahediasi 2012) .
The Shapiro-Wilk Normality Test
- Data: A continuous or discrete sampled variable
- R Function: shapiro.test()
- Null hypothesis (H 0 ): The population distribution from which the sample is drawn is not normal
- History: Samuel Sanford Shapiro and Martin Wilk (1965)
This is an example with random values from a normal distribution.
This is an example with random values from a uniform (non-normal) distribution.
The Kolmogorov-Smirnov Test
The Kolmogorov-Smirnov is a more-generalized test than the Shapiro-Wilks test that can be used to test whether a sample is drawn from any type of distribution.
- Data: A continuous or discrete sampled variable and a reference probability distribution
- R Function: ks.test()
- Null hypothesis (H 0 ): The population distribution from which the sample is drawn does not match the reference distribution
- History: Andrey Kolmogorov (1933) and Nikolai Smirnov (1948)
- pearson.test() The Pearson Chi-square Normality Test from the nortest library. Lower p-values (closer to 0) means to reject the reject the null hypothesis that the distribution IS normal.
Modality Tests of Samples
Comparing two central tendencies: tests with continuous / discrete data, one sample t-test (two-sided).
The one-sample t-test tests the significance of the difference between the mean of a sample and an expected mean.
- Data: A continuous or discrete sampled variable and a single expected mean (μ)
- Parametric (normal distributions)
- R Function: t.test()
- Null hypothesis (H 0 ): The means of the sampled distribution matches the expected mean.
- History: William Sealy Gosset (1908)
t = ( Χ - μ) / (σ̂ / √ n )
- t : The value of t used to find the p-value
- Χ : The sample mean
- μ: The population mean
- σ̂: The estimate of the standard deviation of the population (usually the stdev of the sample
- n : The sample size
T-tests should only be used when the population is at least 20 times larger than its respective sample. If the sample size is too large, the low p-value makes the insignificant look significant. .
For example, we test a hypothesis that the mean weight in IL in 2020 is different than the 2005 continental mean weight.
Walpole et al. (2012) estimated that the average adult weight in North America in 2005 was 178 pounds. We could presume that Illinois is a comparatively normal North American state that would follow the trend of both increased age and increased weight (CDC 2021) .

The low p-value leads us to reject the null hypothesis and corroborate our alternative hypothesis that mean weight changed between 2005 and 2020 in Illinois.
One Sample T-Test (One-Sided)
Because we were expecting an increase, we can modify our hypothesis that the mean weight in 2020 is higher than the continental weight in 2005. We can perform a one-sided t-test using the alternative="greater" parameter.
The low p-value leads us to again reject the null hypothesis and corroborate our alternative hypothesis that mean weight in 2020 is higher than the continental weight in 2005.
Note that this does not clearly evaluate whether weight increased specifically in Illinois, or, if it did, whether that was caused by an aging population or decreasingly healthy diets. Hypotheses based on such questions would require more detailed analysis of individual data.
Although we can see that the mean cancer incidence rate is higher for counties near nuclear plants, there is the possiblity that the difference in means happened by accident and the nuclear plants have nothing to do with those higher rates.
The t-test allows us to test a hypothesis. Note that a t-test does not "prove" or "disprove" anything. It only gives the probability that the differences we see between two areas happened by chance. It also does not evaluate whether there are other problems with the data, such as a third variable, or inaccurate cancer incidence rate estimates.

Note that this does not prove that nuclear power plants present a higher cancer risk to their neighbors. It simply says that the slightly higher risk is probably not due to chance alone. But there are a wide variety of other other related or unrelated social, environmental, or economic factors that could contribute to this difference.
Box-and-Whisker Chart
One visualization commonly used when comparing distributions (collections of numbers) is a box-and-whisker chart. The boxes show the range of values in the middle 25% to 50% to 75% of the distribution and the whiskers show the extreme high and low values.

Although Google Sheets does not provide the capability to create box-and-whisker charts, Google Sheets does have candlestick charts , which are similar to box-and-whisker charts, and which are normally used to display the range of stock price changes over a period of time.
This video shows how to create a candlestick chart comparing the distributions of cancer incidence rates. The QUARTILE() function gets the values that divide the distribution into four equally-sized parts. This shows that while the range of incidence rates in the non-nuclear counties are wider, the bulk of the rates are below the rates in nuclear counties, giving a visual demonstration of the numeric output of our t-test.
While categorical data can often be reduced to dichotomous data and used with proportions tests or t-tests, there are situations where you are sampling data that falls into more than two categories and you would like to make hypothesis tests about those categories. This tutorial describes a group of tests that can be used with that type of data.
Two-Sample T-Test
When comparing means of values from two different groups in your sample, a two-sample t-test is in order.
The two-sample t-test tests the significance of the difference between the means of two different samples.
- Two normally-distributed, continuous or discrete sampled variables, OR
- A normally-distributed continuous or sampled variable and a parallel dichotomous variable indicating what group each of the values in the first variable belong to
- Null hypothesis (H 0 ): The means of the two sampled distributions are equal.
For example, given the low incomes and delicious foods prevalent in Mississippi, we might presume that average weight in Mississippi would be higher than in Illinois.

We test a hypothesis that the mean weight in IL in 2020 is less than the 2020 mean weight in Mississippi.
The low p-value leads us to reject the null hypothesis and corroborate our alternative hypothesis that mean weight in Illinois is less than in Mississippi.
While the difference in means is statistically significant, it is small (182 vs. 187), which should lead to caution in interpretation that you avoid using your analysis simply to reinforce unhelpful stigmatization.
Wilcoxen Rank Sum Test (Mann-Whitney U-Test)
The Wilcoxen rank sum test tests the significance of the difference between the means of two different samples. This is a non-parametric alternative to the t-test.
- Data: Two continuous sampled variables
- Non-parametric (normal or non-normal distributions)
- R Function: wilcox.test()
- Null hypothesis (H 0 ): For randomly selected values X and Y from two populations, the probability of X being greater than Y is equal to the probability of Y being greater than X.
- History: Frank Wilcoxon (1945) and Henry Mann and Donald Whitney (1947)
The test is is implemented with the wilcox.test() function.
- When the test is performed on one sample in comparison to an expected value around which the distribution is symmetrical (μ), the test is known as a Mann-Whitney U test .
- When the test is performed to compare two samples, the test is known as a Wilcoxon rank sum test .
For this example, we will use AVEDRNK3: During the past 30 days, on the days when you drank, about how many drinks did you drink on the average?
- 1 - 76: Number of drinks
- 77: Don’t know/Not sure
- 99: Refused
- NA: Not asked or Missing
The histogram clearly shows this to be a non-normal distribution.

Continuing the comparison of Illinois and Mississippi from above, we might presume that with all that warm weather and excellent food in Mississippi, they might be inclined to drink more. The means of average number of drinks per month seem to suggest that Mississippians do drink more than Illinoians.
We can test use wilcox.test() to test a hypothesis that the average amount of drinking in Illinois is different than in Mississippi. Like the t-test, the alternative can be specified as two-sided or one-sided, and for this example we will test whether the sampled Illinois value is indeed less than the Mississippi value.
The low p-value leads us to reject the null hypothesis and corroborates our hypothesis that average drinking is lower in Illinois than in Mississippi. As before, this tells us nothing about why this is the case.
Weighted Two-Sample T-Test
The downloadable BRFSS data is raw, anonymized survey data that is biased by uneven geographic coverage of survey administration (noncoverage) and lack of responsiveness from some segments of the population (nonresponse). The X_LLCPWT field (landline, cellphone weighting) is a weighting factor added by the CDC that can be assigned to each response to compensate for these biases.
The wtd.t.test() function from the weights library has a weights parameter that can be used to include a weighting factor as part of the t-test.
Comparing Proportions: Tests with Categorical Data
Chi-squared goodness of fit.
- Tests the significance of the difference between sampled frequencies of different values and expected frequencies of those values
- Data: A categorical sampled variable and a table of expected frequencies for each of the categories
- R Function: chisq.test()
- Null hypothesis (H 0 ): The relative proportions of categories in one variable are different from the expected proportions
- History: Karl Pearson (1900)
- Example Question: Are the voting preferences of voters in my district significantly different from the current national polls?
For example, we test a hypothesis that smoking rates changed between 2000 and 2020.
In 2000, the estimated rate of adult smoking in Illinois was 22.3% (Illinois Department of Public Health 2004) .
The variable we will use is SMOKDAY2: Do you now smoke cigarettes every day, some days, or not at all?
- 1: Current smoker - now smokes every day
- 2: Current smoker - now smokes some days
- 3: Not at all
- 7: Don't know
- NA: Not asked or missing - NA is used for people who have never smoked
We subset only yes/no responses in Illinois and convert into a dummy variable (yes = 1, no = 0).
The listing of the table as percentages indicates that smoking rates were halved between 2000 and 2020, but since this is sampled data, we need to run a chi-squared test to make sure the difference can't be explained by the randomness of sampling.
In this case, the very low p-value leads us to reject the null hypothesis and corroborates the alternative hypothesis that smoking rates changed between 2000 and 2020.
Chi-Squared Contingency Analysis / Test of Independence
- Tests the significance of the difference between frequencies between two different groups
- Data: Two categorical sampled variables
- Null hypothesis (H 0 ): The relative proportions of one variable are independent of the second variable.
We can also compare categorical proportions between two sets of sampled categorical variables.
The chi-squared test can is used to determine if two categorical variables are independent. What is passed as the parameter is a contingency table created with the table() function that cross-classifies the number of rows that are in the categories specified by the two categorical variables.
The null hypothesis with this test is that the two categories are independent. The alternative hypothesis is that there is some dependency between the two categories.
For this example, we can compare the three categories of smokers (daily = 1, occasionally = 2, never = 3) across the two categories of states (Illinois and Mississippi).

The low p-value leads us to reject the null hypotheses that the categories are independent and corroborates our hypotheses that smoking behaviors in the two states are indeed different.
p-value = 1.516e-09
Weighted Chi-Squared Contingency Analysis
As with the weighted t-test above, the weights library contains the wtd.chi.sq() function for incorporating weighting into chi-squared contingency analysis.
As above, the even lower p-value leads us to again reject the null hypothesis that smoking behaviors are independent in the two states.
Suppose that the Macrander campaign would like to know how partisan this election is. If people are largely choosing to vote along party lines, the campaign will seek to get their base voters out to the polls. If people are splitting their ticket, the campaign may focus their efforts more broadly.
In the example below, the Macrander campaign took a small poll of 30 people asking who they wished to vote for AND what party they most strongly affiliate with.
The output of table() shows fairly strong relationship between party affiliation and candidates. Democrats tend to vote for Macrander, while Republicans tend to vote for Stewart, while independents all vote for Miller.
This is reflected in the very low p-value from the chi-squared test. This indicates that there is a very low probability that the two categories are independent. Therefore we reject the null hypothesis.
In contrast, suppose that the poll results had showed there were a number of people crossing party lines to vote for candidates outside their party. The simulated data below uses the runif() function to randomly choose 50 party names.
The contingency table() shows no clear relationship between party affiliation and candidate. This is validated quantitatively by the chi-squared test. The fairly high p-value of 0.4018 indicates a 40% chance that the two categories are independent. Therefore, we fail to reject the null hypothesis and the campaign should focus their efforts on the broader electorate.
The warning message given by the chisq.test() function indicates that the sample size is too small to make an accurate analysis. The simulate.p.value = T parameter adds Monte Carlo simulation to the test to improve the estimation and get rid of the warning message. However, the best way to get rid of this message is to get a larger sample.
Comparing Categorical and Continuous Variables
Analysis of variation (anova).
Analysis of Variance (ANOVA) is a test that you can use when you have a categorical variable and a continuous variable. It is a test that considers variability between means for different categories as well as the variability of observations within groups.
There are a wide variety of different extensions of ANOVA that deal with covariance (ANCOVA), multiple variables (MANOVA), and both of those together (MANCOVA). These techniques can become quite complicated and also assume that the values in the continuous variables have a normal distribution.
- Data: One or more categorical (independent) variables and one continuous (dependent) sampled variable
- R Function: aov()
- Null hypothesis (H 0 ): There is no difference in means of the groups defined by each level of the categorical (independent) variable
- History: Ronald Fisher (1921)
- Example Question: Do low-, middle- and high-income people vary in the amount of time they spend watching TV?
As an example, we look at the continuous weight variable (WEIGHT2) split into groups by the eight income categories in INCOME2: Is your annual household income from all sources?
- 1: Less than $10,000
- 2: $10,000 to less than $15,000
- 3: $15,000 to less than $20,000
- 4: $20,000 to less than $25,000
- 5: $25,000 to less than $35,000
- 6: $35,000 to less than $50,000
- 7: $50,000 to less than $75,000)
- 8: $75,000 or more
The barplot() of means does show variation among groups, although there is no clear linear relationship between income and weight.

To test whether this variation could be explained by randomness in the sample, we run the ANOVA test.
The low p-value leads us to reject the null hypothesis that there is no difference in the means of the different groups, and corroborates the alternative hypothesis that mean weights differ based on income group.
However, it gives us no clear model for describing that relationship and offers no insights into why income would affect weight, especially in such a nonlinear manner.
Suppose you are performing research into obesity in your city. You take a sample of 30 people in three different neighborhoods (90 people total), collecting information on health and lifestyle. Two variables you collect are height and weight so you can calculate body mass index . Although this index can be misleading for some populations (notably very athletic people), ordinary sedentary people can be classified according to BMI:
Average BMI in the US from 2007-2010 was around 28.6 and rising, standard deviation of around 5 .
You would like to know if there is a difference in BMI between different neighborhoods so you can know whether to target specific neighborhoods or make broader city-wide efforts. Since you have more than two groups, you cannot use a t-test().
Kruskal-Wallace One-Way Analysis of Variance
A somewhat simpler test is the Kruskal-Wallace test which is a nonparametric analogue to ANOVA for testing the significance of differences between two or more groups.
- R Function: kruskal.test()
- Null hypothesis (H 0 ): The samples come from the same distribution.
- History: William Kruskal and W. Allen Wallis (1952)
For this example, we will investigate whether mean weight varies between the three major US urban states: New York, Illinois, and California.

To test whether this variation could be explained by randomness in the sample, we run the Kruskal-Wallace test.
The low p-value leads us to reject the null hypothesis that the samples come from the same distribution. This corroborates the alternative hypothesis that mean weights differ based on state.
A convienent way of visualizing a comparison between continuous and categorical data is with a box plot , which shows the distribution of a continuous variable across different groups:

A percentile is the level at which a given percentage of the values in the distribution are below: the 5th percentile means that five percent of the numbers are below that value.
The quartiles divide the distribution into four parts. 25% of the numbers are below the first quartile. 75% are below the third quartile. 50% are below the second quartile, making it the median.
Box plots can be used with both sampled data and population data.
The first parameter to the box plot is a formula: the continuous variable as a function of (the tilde) the second variable. A data= parameter can be added if you are using variables in a data frame.
The chi-squared test can be used to determine if two categorical variables are independent of each other.
Introduction to Statistics with R
6.2 hypothesis tests, 6.2.1 illustrating a hypothesis test.
Let’s say we have a batch of chocolate bars, and we’re not sure if they are from Theo’s. What can the weight of these bars tell us about the probability that these are Theo’s chocolate?
Now, let’s perform a hypothesis test on this chocolate of an unknown origin.
What is the sampling distribution of the bar weight under the null hypothesis that the bars from Theo’s weigh 40 grams on average? We’ll need to specify the standard deviation to obtain the sampling distribution, and here we’ll use \(\sigma_X = 2\) (since that’s the value we used for the distribution we sampled from).
The null hypothesis is \[H_0: \mu = 40\] since we know the mean weight of Theo’s chocolate bars is 40 grams.
The sample distribution of the sample mean is: \[ \overline{X} \sim {\cal N}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) = {\cal N}\left(40, \frac{2}{\sqrt{20}}\right). \] We can visualize the situation by plotting the p.d.f. of the sampling distribution under \(H_0\) along with the location of our observed sample mean.

6.2.2 Hypothesis Tests for Means
6.2.2.1 known standard deviation.
It is simple to calculate a hypothesis test in R (in fact, we already implicitly did this in the previous section). When we know the population standard deviation, we use a hypothesis test based on the standard normal, known as a \(z\) -test. Here, let’s assume \(\sigma_X = 2\) (because that is the standard deviation of the distribution we simulated from above) and specify the alternative hypothesis to be \[ H_A: \mu \neq 40. \] We will the z.test() function from the BSDA package, specifying the confidence level via conf.level , which is \(1 - \alpha = 1 - 0.05 = 0.95\) , for our test:
6.2.2.2 Unknown Standard Deviation
If we do not know the population standard deviation, we typically use the t.test() function included in base R. We know that: \[\frac{\overline{X} - \mu}{\frac{s_x}{\sqrt{n}}} \sim t_{n-1},\] where \(t_{n-1}\) denotes Student’s \(t\) distribution with \(n - 1\) degrees of freedom. We only need to supply the confidence level here:
We note that the \(p\) -value here (rounded to 4 decimal places) is 0.0031, so again, we can detect it’s not likely that these bars are from Theo’s. Even with a very small sample, the difference is large enough (and the standard deviation small enough) that the \(t\) -test can detect it.
6.2.3 Two-sample Tests
6.2.3.1 unpooled two-sample t-test.
Now suppose we have two batches of chocolate bars, one of size 40 and one of size 45. We want to test whether they come from the same factory. However we have no information about the distributions of the chocolate bars. Therefore, we cannot conduct a one sample t-test like above as that would require some knowledge about \(\mu_0\) , the population mean of chocolate bars.
We will generate the samples from normal distribution with mean 45 and 47 respectively. However, let’s assume we do not know this information. The population standard deviation of the distributions we are sampling from are both 2, but we will assume we do not know that either. Let us denote the unknown true population means by \(\mu_1\) and \(\mu_2\) .

Consider the test \(H_0:\mu_1=\mu_2\) versus \(H_1:\mu_1\neq\mu_2\) . We can use R function t.test again, since this function can perform one- and two-sided tests. In fact, t.test assumes a two-sided test by default, so we do not have to specify that here.
The p-value is much less than .05, so we can quite confidently reject the null hypothesis. Indeed, we know from simulating the data that \(\mu_1\neq\mu_2\) , so our test led us to the correct conclusion!
Consider instead testing \(H_0:\mu_1=\mu_2\) versus \(H_1:\mu_1\leq\mu_2\) .
As we would expect, this test also rejects the null hypothesis. One-sided tests are more common in practice as they provide a more principled description of the relationship between the datasets. For example, if you are comparing your new drug’s performance to a “gold standard”, you really only care if your drug’s performance is “better” (a one-sided alternative), and not that your drug’s performance is merely “different” (a two-sided alternative).
6.2.3.2 Pooled Two-sample t-test
Suppose you knew that the samples are coming from distributions with same standard deviations. Then it makes sense to carry out a pooled 2 sample t-test. You specify this in the t.test function as follows.
6.2.3.3 Paired t-test
Suppose we take a batch of chocolate bars and stamp the Theo’s logo on them. We want to know if the stamping process significantly changes the weight of the chocolate bars. Let’s suppose that the true change in weight is distributed as a \({\cal N}(-0.3, 0.2^2)\) random variable:

Let \(\mu_1\) and \(\mu_2\) be the true means of the distributions of chocolate weights before and after the stamping process. Suppose we want to test \(H_0:\mu_1=\mu_2\) versus \(\mu_1\neq\mu_2\) . We can use the R function t.test() for this by choosing paired = TRUE , which indicates that we are looking at pairs of observations corresponding to the same experimental subject and testing whether or not the difference in distribution means is zero.
We can also perform the same test as a one sample t-test using choc.after - choc.batch .
Notice that we get the exact same \(p\) -value for these two tests.
Since the p-value is less than .05, we reject the null hypothesis at level .05. Hence, we have enough evidence in the data to claim that stamping a chocolate bar significantly reduces its weight.
6.2.4 Tests for Proportions
Let’s look at the proportion of Theo’s chocolate bars with a weight exceeding 38g:
Going back to that first batch of 20 chocolate bars of unknown origin, let’s see if we can test whether they’re from Theo’s based on the proportion weighing > 38g.
Recall from our test on the means that we rejected the null hypothesis that the means from the two batches were equal. In this case, a one-sided test is appropiate, and our hypothesis is:
Null hypothesis: \(H_0: p = 0.85\) . Alternative: \(H_A: p > 0.85\) .
We want to test this hypothesis at a level \(\alpha = 0.05\) .
In R, there is a function called prop.test() that you can use to perform tests for proportions. Note that prop.test() only gives you an approximate result.
Similarly, you can use the binom.test() function for an exact result.
The \(p\) -value for both tests is around 0.18, which is much greater than 0.05. So, we cannot reject the hypothesis that the unknown bars come from Theo’s. This is not because the tests are less accurate than the ones we ran before, but because we are testing a less sensitive measure: the proportion weighing > 38 grams, rather than the mean weights. Also, note that this doesn’t mean that we can conclude that these bars do come from Theo’s – why not?
The prop.test() function is the more versatile function in that it can deal with contingency tables, larger number of groups, etc. The binom.test() function gives you exact results, but you can only apply it to one-sample questions.
6.2.5 Power
Let’s think about when we reject the null hypothesis. We would reject the null hypothesis if we observe data with too small of a \(p\) -value. We can calculate the critical value where we would reject the null if we were to observe data that would lead to a more extreme value.
Suppose we take a sample of chocolate bars of size n = 20 , and our null hypothesis is that the bars come from Theo’s ( \(H_0\) : mean = 40, sd = 2 ). Then for a one-sided test (versus larger alternatives), we can calculate the critical value by using the quantile function in R, specifiying the mean and sd of the sampling distribution of \(\overline X\) under \(H_0\) :
Now suppose we want to calculate the power of our hypothesis test: the probability of rejecting the null hypothesis when the null hypothesis is false. In order to do so, we need to compare the null to a specific alternative, so we choose \(H_A\) : mean = 42, sd = 2 . Then the probability that we reject the null under this specific alternative is
We can use R to perform the same calculations using the power.z.test from the asbio package:
| linear.hypothesis {car} | R Documentation |
Test Linear Hypothesis
Description.
Generic function for testing a linear hypothesis, and methods for linear models, generalized linear models, and other models that have methods for coef and vcov .
| fitted model object. The default method works for models for which the estimated parameters can be retrieved by and the corresponding estimated covariance matrix by . See the for more information. | |
| matrix (or vector) giving linear combinations of coefficients by rows, or a character vector giving the hypothesis in symbolic form (see ). | |
| right-hand-side vector for hypothesis, with as many entries as rows in the hypothesis matrix; can be omitted, in which case it defaults to a vector of zeroes. | |
| character specifying whether to compute the finite sample F statistic (with approximate F distribution) or the large sample Chi-squared statistic (with asymptotic Chi-squared distribution). | |
| a function for estimating the covariance matrix of the regression coefficients, e.g., , or an estimated covariance matrix for . See also . | |
| logical or character. Convenience interface to (instead of using the argument ). Can be set either to a character specifying the argument of or , in which case is used implicitly. For backwards compatibility. | |
| If , the hypothesis matrix and right-hand-side vector are printed to standard output; if (the default), the hypothesis is only printed in symbolic form. | |
| aruments to pass down. |
Computes either a finite sample F statistic or asymptotic Chi-squared statistic for carrying out a Wald-test-based comparison between a model and a linearly restricted model. The default method will work with any model object for which the coefficient vector can be retrieved by coef and the coefficient-covariance matrix by vcov (otherwise the argument vcov. has to be set explicitely). For computing the F statistic (but not the Chi-squared statistic) a df.residual method needs to be available. If a formula method exists, it is used for pretty printing.
The method for "lm" objects calls the default method, but it changes the default test to "F" , supports the convenience argument white.adjust (for backwards compatibility), and enhances the output by residual sums of squares. For "glm" objects just the default method is called (bypassing the "lm" method).
The function lht also dispatches to linear.hypothesis .
The hypothesis matrix can be supplied as a numeric matrix (or vector), the rows of which specify linear combinations of the model coefficients, which are tested equal to the corresponding entries in the righ-hand-side vector, which defaults to a vector of zeroes.
Alternatively, the hypothesis can be specified symbolically as a character vector with one or more elements, each of which gives either a linear combination of coefficients, or a linear equation in the coefficients (i.e., with both a left and right side separated by an equals sign). Components of a linear expression or linear equation can consist of numeric constants, or numeric constants multiplying coefficient names (in which case the number precedes the coefficient, and may be separated from it by spaces or an asterisk); constants of 1 or -1 may be omitted. Spaces are always optional. Components are separated by positive or negative signs. See the examples below.
An object of class "anova" which contains the residual degrees of freedom in the model, the difference in degrees of freedom, Wald statistic (either "F" or "Chisq" ) and corresponding p value.
Achim Zeleis and John Fox [email protected]
Fox, J. (1997) Applied Regression, Linear Models, and Related Methods. Sage.
anova , Anova , waldtest , hccm , vcovHC , vcovHAC , coef , vcov
![Cohansey River, Fairfield, New Jersey [banner]](https://rcompanion.org/images/banner.jpg)
Summary and Analysis of Extension Program Evaluation in R
Salvatore S. Mangiafico
Search Rcompanion.org
- Purpose of this Book
- Author of this Book
- Statistics Textbooks and Other Resources
- Why Statistics?
- Evaluation Tools and Surveys
- Types of Variables
- Descriptive Statistics
- Confidence Intervals
- Basic Plots
Hypothesis Testing and p-values
- Reporting Results of Data and Analyses
- Choosing a Statistical Test
- Independent and Paired Values
- Introduction to Likert Data
- Descriptive Statistics for Likert Item Data
- Descriptive Statistics with the likert Package
- Confidence Intervals for Medians
- Converting Numeric Data to Categories
- Introduction to Traditional Nonparametric Tests
- One-sample Wilcoxon Signed-rank Test
- Sign Test for One-sample Data
- Two-sample Mann–Whitney U Test
- Mood’s Median Test for Two-sample Data
- Two-sample Paired Signed-rank Test
- Sign Test for Two-sample Paired Data
- Kruskal–Wallis Test
- Mood’s Median Test
- Friedman Test
- Scheirer–Ray–Hare Test
- Aligned Ranks Transformation ANOVA
- Nonparametric Regression and Local Regression
- Nonparametric Regression for Time Series
- Introduction to Permutation Tests
- One-way Permutation Test for Ordinal Data
- One-way Permutation Test for Paired Ordinal Data
- Permutation Tests for Medians and Percentiles
- Association Tests for Ordinal Tables
- Measures of Association for Ordinal Tables
- Introduction to Linear Models
- Using Random Effects in Models
- What are Estimated Marginal Means?
- Estimated Marginal Means for Multiple Comparisons
- Factorial ANOVA: Main Effects, Interaction Effects, and Interaction Plots
- p-values and R-square Values for Models
- Accuracy and Errors for Models
- Introduction to Cumulative Link Models (CLM) for Ordinal Data
- Two-sample Ordinal Test with CLM
- Two-sample Paired Ordinal Test with CLMM
- One-way Ordinal Regression with CLM
- One-way Repeated Ordinal Regression with CLMM
- Two-way Ordinal Regression with CLM
- Two-way Repeated Ordinal Regression with CLMM
- Introduction to Tests for Nominal Variables
- Confidence Intervals for Proportions
- Goodness-of-Fit Tests for Nominal Variables
- Association Tests for Nominal Variables
- Measures of Association for Nominal Variables
- Tests for Paired Nominal Data
- Cochran–Mantel–Haenszel Test for 3-Dimensional Tables
- Cochran’s Q Test for Paired Nominal Data
- Models for Nominal Data
- Introduction to Parametric Tests
- One-sample t-test
- Two-sample t-test
- Paired t-test
- One-way ANOVA
- One-way ANOVA with Blocks
- One-way ANOVA with Random Blocks
- Two-way ANOVA
- Repeated Measures ANOVA
- Correlation and Linear Regression
- Advanced Parametric Methods
- Transforming Data
- Normal Scores Transformation
- Regression for Count Data
- Beta Regression for Percent and Proportion Data
- An R Companion for the Handbook of Biological Statistics
Initial comments
Traditionally when students first learn about the analysis of experiments, there is a strong focus on hypothesis testing and making decisions based on p -values. Hypothesis testing is important for determining if there are statistically significant effects. However, readers of this book should not place undo emphasis on p -values. Instead, they should realize that p -values are affected by sample size, and that a low p -value does not necessarily suggest a large effect or a practically meaningful effect. Summary statistics, plots, effect size statistics, and practical considerations should be used. The goal is to determine: a) statistical significance, b) effect size, c) practical importance. These are all different concepts, and they will be explored below.
Statistical inference
Most of what we’ve covered in this book so far is about producing descriptive statistics: calculating means and medians, plotting data in various ways, and producing confidence intervals. The bulk of the rest of this book will cover statistical inference: using statistical tests to draw some conclusion about the data. We’ve already done this a little bit in earlier chapters by using confidence intervals to conclude if means are different or not among groups.
As Dr. Nic mentions in her article in the “References and further reading” section, this is the part where people sometimes get stumped. It is natural for most of us to use summary statistics or plots, but jumping to statistical inference needs a little change in perspective. The idea of using some statistical test to answer a question isn’t a difficult concept, but some of the following discussion gets a little theoretical. The video from the Statistics Learning Center in the “References and further reading” section does a good job of explaining the basis of statistical inference.
One important thing to gain from this chapter is an understanding of how to use the p -value, alpha , and decision rule to test the null hypothesis. But once you are comfortable with that, you will want to return to this chapter to have a better understanding of the theory behind this process.
Another important thing is to understand the limitations of relying on p -values, and why it is important to assess the size of effects and weigh practical considerations.
Packages used in this chapter
The packages used in this chapter include:
The following commands will install these packages if they are not already installed:
if(!require(lsr)){install.packages("lsr")}
Hypothesis testing
The null and alternative hypotheses.
The statistical tests in this book rely on testing a null hypothesis, which has a specific formulation for each test. The null hypothesis always describes the case where e.g. two groups are not different or there is no correlation between two variables, etc.
The alternative hypothesis is the contrary of the null hypothesis, and so describes the cases where there is a difference among groups or a correlation between two variables, etc.
Notice that the definitions of null hypothesis and alternative hypothesis have nothing to do with what you want to find or don't want to find, or what is interesting or not interesting, or what you expect to find or what you don’t expect to find. If you were comparing the height of men and women, the null hypothesis would be that the height of men and the height of women were not different. Yet, you might find it surprising if you found this hypothesis to be true for some population you were studying. Likewise, if you were studying the income of men and women, the null hypothesis would be that the income of men and women are not different, in the population you are studying. In this case you might be hoping the null hypothesis is true, though you might be unsurprised if the alternative hypothesis were true. In any case, the null hypothesis will take the form that there is no difference between groups, there is no correlation between two variables, or there is no effect of this variable in our model.
p -value definition
Most of the tests in this book rely on using a statistic called the p -value to evaluate if we should reject, or fail to reject, the null hypothesis.
Given the assumption that the null hypothesis is true , the p -value is defined as the probability of obtaining a result equal to or more extreme than what was actually observed in the data.
We’ll unpack this definition in a little bit.
Decision rule
The p -value for the given data will be determined by conducting the statistical test.
This p -value is then compared to a pre-determined value alpha . Most commonly, an alpha value of 0.05 is used, but there is nothing magic about this value.
If the p -value for the test is less than alpha , we reject the null hypothesis.
If the p -value is greater than or equal to alpha , we fail to reject the null hypothesis.
Coin flipping example
For an example of using the p -value for hypothesis testing, imagine you have a coin you will toss 100 times. The null hypothesis is that the coin is fair—that is, that it is equally likely that the coin will land on heads as land on tails. The alternative hypothesis is that the coin is not fair. Let’s say for this experiment you throw the coin 100 times and it lands on heads 95 times out of those hundred. The p -value in this case would be the probability of getting 95, 96, 97, 98, 99, or 100 heads, or 0, 1, 2, 3, 4, or 5 heads, assuming that the null hypothesis is true .
This is what we call a two-sided test, since we are testing both extremes suggested by our data: getting 95 or greater heads or getting 95 or greater tails. In most cases we will use two sided tests.
You can imagine that the p -value for this data will be quite small. If the null hypothesis is true, and the coin is fair, there would be a low probability of getting 95 or more heads or 95 or more tails.
Using a binomial test, the p -value is < 0.0001.
(Actually, R reports it as < 2.2e-16, which is shorthand for the number in scientific notation, 2.2 x 10 -16 , which is 0.00000000000000022, with 15 zeros after the decimal point.)
Assuming an alpha of 0.05, since the p -value is less than alpha , we reject the null hypothesis. That is, we conclude that the coin is not fair.
binom.test(5, 100, 0.5)
Exact binomial test number of successes = 5, number of trials = 100, p-value < 2.2e-16 alternative hypothesis: true probability of success is not equal to 0.5
Passing and failing example
As another example, imagine we are considering two classrooms, and we have counts of students who passed a certain exam. We want to know if one classroom had statistically more passes or failures than the other.
In our example each classroom will have 10 students. The data is arranged into a contingency table.
Classroom Passed Failed A 8 2 B 3 7
We will use Fisher’s exact test to test if there is an association between Classroom and the counts of passed and failed students. The null hypothesis is that there is no association between Classroom and Passed/Failed , based on the relative counts in each cell of the contingency table.
Input =(" Classroom Passed Failed A 8 2 B 3 7 ") Matrix = as.matrix(read.table(textConnection(Input), header=TRUE, row.names=1)) Matrix
Passed Failed A 8 2 B 3 7
fisher.test(Matrix)
Fisher's Exact Test for Count Data p-value = 0.06978
The reported p -value is 0.070. If we use an alpha of 0.05, then the p -value is greater than alpha , so we fail to reject the null hypothesis. That is, we did not have sufficient evidence to say that there is an association between Classroom and Passed/Failed .
More extreme data in this case would be if the counts in the upper left or lower right (or both!) were greater.
Classroom Passed Failed A 9 1 B 3 7 Classroom Passed Failed A 10 0 B 3 7 and so on, with Classroom B...
In most cases we would want to consider as "extreme" not only the results when Classroom A has a high frequency of passing students, but also results when Classroom B has a high frequency of passing students. This is called a two-sided or two-tailed test. If we were only concerned with one classroom having a high frequency of passing students, relatively, we would instead perform a one-sided test. The default for the fisher.test function is two-sided, and usually you will want to use two-sided tests.
Classroom Passed Failed A 2 8 B 7 3 Classroom Passed Failed A 1 9 B 7 3 Classroom Passed Failed A 0 10 B 7 3 and so on, with Classroom B...
In both cases, "extreme" means there is a stronger association between Classroom and Passed/Failed .
Theory and practice of using p -values
Wait, does this make any sense.
Recall that the definition of the p -value is:
The astute reader might be asking herself, “If I’m trying to determine if the null hypothesis is true or not, why would I start with the assumption that the null hypothesis is true? And why am I using a probability of getting certain data given that a hypothesis is true? Don’t I want to instead determine the probability of the hypothesis given my data?”
The answer is yes , we would like a method to determine the likelihood of our hypothesis being true given our data, but we use the Null Hypothesis Significance Test approach since it is relatively straightforward, and has wide acceptance historically and across disciplines.
In practice we do use the results of the statistical tests to reach conclusions about the null hypothesis.
Technically, the p -value says nothing about the alternative hypothesis. But logically, if the null hypothesis is rejected, then its logical complement, the alternative hypothesis, is supported. Practically, this is how we handle significant p -values, though this practical approach generates disapproval in some theoretical circles.
Statistics is like a jury?
Note the language used when testing the null hypothesis. Based on the results of our statistical tests, we either reject the null hypothesis, or fail to reject the null hypothesis.
This is somewhat similar to the approach of a jury in a trial. The jury either finds sufficient evidence to declare someone guilty, or fails to find sufficient evidence to declare someone guilty.
Failing to convict someone isn’t necessarily the same as declaring someone innocent. Likewise, if we fail to reject the null hypothesis, we shouldn’t assume that the null hypothesis is true. It may be that we didn’t have sufficient samples to get a result that would have allowed us to reject the null hypothesis, or maybe there are some other factors affecting the results that we didn’t account for. This is similar to an “innocent until proven guilty” stance.
Errors in inference
For the most part, the statistical tests we use are based on probability, and our data could always be the result of chance. Considering the coin flipping example above, if we did flip a coin 100 times and came up with 95 heads, we would be compelled to conclude that the coin was not fair. But 95 heads could happen with a fair coin strictly by chance.
We can, therefore, make two kinds of errors in testing the null hypothesis:
• A Type I error occurs when the null hypothesis really is true, but based on our decision rule we reject the null hypothesis. In this case, our result is a false positive ; we think there is an effect (unfair coin, association between variables, difference among groups) when really there isn’t. The probability of making this kind error is alpha , the same alpha we used in our decision rule.
• A Type II error occurs when the null hypothesis is really false, but based on our decision rule we fail to reject the null hypothesis. In this case, our result is a false negative ; we have failed to find an effect that really does exist. The probability of making this kind of error is called beta .
The following table summarizes these errors.
Reality ___________________________________ Decision of Test Null is true Null is false Reject null hypothesis Type I error Correctly (prob. = alpha) reject null (prob. = 1 – beta) Retain null hypothesis Correctly Type II error retain null (prob. = beta) (prob. = 1 – alpha)
Statistical power
The statistical power of a test is a measure of the ability of the test to detect a real effect. It is related to the effect size, the sample size, and our chosen alpha level.
The effect size is a measure of how unfair a coin is, how strong the association is between two variables, or how large the difference is among groups. As the effect size increases or as the number of observations we collect increases, or as the alpha level increases, the power of the test increases.
Statistical power in the table above is indicated by 1 – beta , and power is the probability of correctly rejecting the null hypothesis.
An example should make these relationship clear. Imagine we are sampling a large group of 7 th grade students for their height. That is, the group is the population, and we are sampling a sub-set of these students. In reality, for students in the population, the girls are taller than the boys, but the difference is small (that is, the effect size is small), and there is a lot of variability in students’ heights. You can imagine that in order to detect the difference between girls and boys that we would have to measure many students. If we fail to sample enough students, we might make a Type II error. That is, we might fail to detect the actual difference in heights between sexes.
If we had a different experiment with a larger effect size—for example the weight difference between mature hamsters and mature hedgehogs—we might need fewer samples to detect the difference.
Note also, that our chosen alpha plays a role in the power of our test, too. All things being equal, across many tests, if we decrease our alph a, that is, insist on a lower rate of Type I errors, we are more likely to commit a Type II error, and so have a lower power. This is analogous to a case of a meticulous jury that has a very high standard of proof to convict someone. In this case, the likelihood of a false conviction is low, but the likelihood of a letting a guilty person go free is relatively high.
The 0.05 alpha value is not dogma
The level of alpha is traditionally set at 0.05 in some disciplines, though there is sometimes reason to choose a different value.
One situation in which the alpha level is increased is in preliminary studies in which it is better to include potentially significant effects even if there is not strong evidence for keeping them. In this case, the researcher is accepting an inflated chance of Type I errors in order to decrease the chance of Type II errors.
Imagine an experiment in which you wanted to see if various environmental treatments would improve student learning. In a preliminary study, you might have many treatments, with few observations each, and you want to retain any potentially successful treatments for future study. For example, you might try playing classical music, improved lighting, complimenting students, and so on, and see if there is any effect on student learning. You might relax your alpha value to 0.10 or 0.15 in the preliminary study to see what treatments to include in future studies.
On the other hand, in situations where a Type I, false positive, error might be costly in terms of money or people’s health, a lower alpha can be used, perhaps, 0.01 or 0.001. You can imagine a case in which there is an established treatment for cancer, and a new treatment is being tested. Because the new treatment is likely to be expensive and to hold people’s lives in the balance, a researcher would want to be very sure that the new treatment is more effective than the established treatment. In reality, the researchers would not just lower the alpha level, but also look at the effect size, submit the research for peer review, replicate the study, be sure there were no problems with the design of the study or the data collection, and weigh the practical implications.
The 0.05 alpha value is almost dogma
In theory, as a researcher, you would determine the alpha level you feel is appropriate. That is, the probability of making a Type I error when the null hypothesis is in fact true.
In reality, though, 0.05 is almost always used in most fields for readers of this book. Choosing a different alpha value will rarely go without question. It is best to keep with the 0.05 level unless you have good justification for another value, or are in a discipline where other values are routinely used.
Practical advice
One good practice is to report actual p -values from analyses. It is fine to also simply say, e.g. “The dependent variable was significantly correlated with variable A ( p < 0.05).” But I prefer when possible to say, “The dependent variable was significantly correlated with variable A ( p = 0.026).
It is probably best to avoid using terms like “marginally significant” or “borderline significant” for p -values less than 0.10 but greater than 0.05, though you might encounter similar phrases. It is better to simply report the p -values of tests or effects in straight-forward manner. If you had cause to include certain model effects or results from other tests, they can be reported as e.g., “Variables correlated with the dependent variable with p < 0.15 were A , B , and C .”
Is the p -value every really true?
Considering some of the examples presented, it may have occurred to the reader to ask if the null hypothesis is ever really true. For example, in some population of 7 th graders, if we could measure everyone in the population to a high degree of precision, then there must be some difference in height between girls and boys. This is an important limitation of null hypothesis significance testing. Often, if we have many observations, even small effects will be reported as significant. This is one reason why it is important to not rely too heavily on p -values, but to also look at the size of the effect and practical considerations. In this example, if we sampled many students and the difference in heights was 0.5 cm, even if significant, we might decide that this effect is too small to be of practical importance, especially relative to an average height of 150 cm. (Here, the difference would be 0.3% of the average height).
Effect sizes and practical importance
Practical importance and statistical significance.
It is important to remember to not let p -values be the only guide for drawing conclusions. It is equally important to look at the size of the effects you are measuring, as well as take into account other practical considerations like the costs of choosing a certain path of action.
For example, imagine we want to compare the SAT scores of two SAT preparation classes with a t -test.
Class.A = c(1500, 1505, 1505, 1510, 1510, 1510, 1515, 1515, 1520, 1520) Class.B = c(1510, 1515, 1515, 1520, 1520, 1520, 1525, 1525, 1530, 1530) t.test(Class.A, Class.B)
Welch Two Sample t-test t = -3.3968, df = 18, p-value = 0.003214 mean of x mean of y 1511 1521
The p -value is reported as 0.003, so we would consider there to be a significant difference between the two classes ( p < 0.05).
But we have to ask ourselves the practical question, is a difference of 10 points on the SAT large enough for us to care about? What if enrolling in one class costs significantly more than the other class? Is it worth the extra money for a difference of 10 points on average?
Sizes of effects
It should be remembered that p -values do not indicate the size of the effect being studied. It shouldn’t be assumed that a small p -value indicates a large difference between groups, or vice-versa.
For example, in the SAT example above, the p -value is fairly small, but the size of the effect (difference between classes) in this case is relatively small (10 points, especially small relative to the range of scores students receive on the SAT).
In converse, there could be a relatively large size of the effects, but if there is a lot of variability in the data or the sample size is not large enough, the p -value could be relatively large.
In this example, the SAT scores differ by 100 points between classes, but because the variability is greater than in the previous example, the p -value is not significant.
Class.C = c(1000, 1100, 1200, 1250, 1300, 1300, 1400, 1400, 1450, 1500) Class.D = c(1100, 1200, 1300, 1350, 1400, 1400, 1500, 1500, 1550, 1600) t.test(Class.C, Class.D)
Welch Two Sample t-test t = -1.4174, df = 18, p-value = 0.1735 mean of x mean of y 1290 1390
boxplot(cbind(Class.C, Class.D))

p -values and sample sizes
It should also be remembered that p -values are affected by sample size. For a given effect size and variability in the data, as the sample size increases, the p -value is likely to decrease. For large data sets, small effects can result in significant p -values.
As an example, let’s take the data from Class.C and Class.D and double the number of observations for each without changing the distribution of the values in each, and rename them Class.E and Class.F .
Class.E = c(1000, 1100, 1200, 1250, 1300, 1300, 1400, 1400, 1450, 1500, 1000, 1100, 1200, 1250, 1300, 1300, 1400, 1400, 1450, 1500) Class.F = c(1100, 1200, 1300, 1350, 1400, 1400, 1500, 1500, 1550, 1600, 1100, 1200, 1300, 1350, 1400, 1400, 1500, 1500, 1550, 1600) t.test(Class.E, Class.F)
Welch Two Sample t-test t = -2.0594, df = 38, p-value = 0.04636 mean of x mean of y 1290 1390
boxplot(cbind(Class.E, Class.F))
Notice that the p -value is lower for the t -test for Class.E and Class.F than it was for Class.C and Class.D . Also notice that the means reported in the output are the same, and the box plots would look the same.
Effect size statistics
One way to account for the effect of sample size on our statistical tests is to consider effect size statistics. These statistics reflect the size of the effect in a standardized way, and are unaffected by sample size.
An appropriate effect size statistic for a t -test is Cohen’s d . It takes the difference in means between the two groups and divides by the pooled standard deviation of the groups. Cohen’s d equals zero if the means are the same, and increases to infinity as the difference in means increases relative to the standard deviation.
In the following, note that Cohen’s d is not affected by the sample size difference in the Class.C / Class.D and the Class.E / Class.F examples.
library(lsr) cohensD(Class.C, Class.D, method = "raw")
cohensD(Class.E, Class.F, method = "raw")
Effect size statistics are standardized so that they are not affected by the units of measurements of the data. This makes them interpretable across different situations, or if the reader is not familiar with the units of measurement in the original data. A Cohen’s d of 1 suggests that the two means differ by one pooled standard deviation. A Cohen’s d of 0.5 suggests that the two means differ by one-half the pooled standard deviation.
For example, if we create new variables— Class.G and Class.H —that are the SAT scores from the previous example expressed as a proportion of a 1600 score, Cohen’s d will be the same as in the previous example.
Class.G = Class.E / 1600 Class.H = Class.F / 1600 Class.G Class.H cohensD(Class.G, Class.H, method="raw")
Good practices for statistical analyses
Statistics is not like a trial.
When analyzing data, the analyst should not approach the task as would a lawyer for the prosecution. That is, the analyst should not be searching for significant effects and tests, but should instead be like an independent investigator using lines of evidence to find out what is most likely to true given the data, graphical analysis, and statistical analysis available.
The problem of multiple p -values
One concept that will be in important in the following discussion is that when there are multiple tests producing multiple p -values, that there is an inflation of the Type I error rate. That is, there is a higher chance of making false-positive errors.
This simply follows mathematically from the definition of alpha . If we allow a probability of 0.05, or 5% chance, of making a Type I error for any one test, as we do more and more tests, the chances that at least one of them having a false positive becomes greater and greater.
p -value adjustment
One way we deal with the problem of multiple p -values in statistical analyses is to adjust p -values when we do a series of tests together (for example, if we are comparing the means of multiple groups).
Don’t use Bonferroni adjustments
There are various p -value adjustments available in R. In some cases, we will use FDR, which stands for false discovery rate , and in R is an alias for the Benjamini and Hochberg method. There are also cases in which we’ll use Tukey range adjustment to correct for the family-wise error rate.
Unfortunately, students in analysis of experiments courses often learn to use Bonferroni adjustment for p -values. This method is simple to do with hand calculations, but is excessively conservative in most situations, and, in my opinion, antiquated.
There are other p -value adjustment methods, and the choice of which one to use is dictated either by which are common in your field of study, or by doing enough reading to understand which are statistically most appropriate for your application.
Preplanned tests
The statistical tests covered in this book assume that tests are preplanned for their p -values to be accurate. That is, in theory, you set out an experiment, collect the data as planned, and then say “I’m going to analyze it with kind of model and do these post-hoc tests afterwards”, and report these results, and that’s all you would do.
Some authors emphasize this idea of preplanned tests. In contrast is an exploratory data analysis approach that relies upon examining the data with plots and using simple tests like correlation tests to suggest what statistical analysis makes sense.
If an experiment is set out in a specific design, then usually it is appropriate to use the analysis suggested by this design.

p -value hacking
It is important when approaching data from an exploratory approach, to avoid committing p -value hacking. Imagine the case in which the researcher collects many different measurements across a range of subjects. The researcher might be tempted to simply try different tests and models to relate one variable to another, for all the variables. He might continue to do this until he found a test with a significant p -value.
But this would be a form of p -value hacking.
Because an alpha value of 0.05 allows us to make a false-positive error five percent of the time, finding one p -value below 0.05 after several successive tests may simply be due to chance.
Some forms of p -value hacking are more egregious. For example, if one were to collect some data, run a test, and then continue to collect data and run tests iteratively until a significant p -value is found.
Publication bias
A related issue in science is that there is a bias to publish, or to report, only significant results. This can also lead to an inflation of the false-positive rate. As a hypothetical example, imagine if there are currently 20 similar studies being conducted testing a similar effect—let’s say the effect of glucosamine supplements on joint pain. If 19 of those studies found no effect and so were discarded, but one study found an effect using an alpha of 0.05, and was published, is this really any support that glucosamine supplements decrease joint pain?
Clarification of terms and reporting on assignments
"statistically significant".
In the context of this book, the term "significant" means "statistically significant".
Whenever the decision rule finds that p < alpha , the difference in groups, the association, or the correlation under consideration is then considered "statistically significant" or "significant".
No effect size or practical considerations enter into determining whether an effect is “significant” or not. The only exception is that test assumptions and requirements for appropriate data must also be met in order for the p -value to be valid.
What you need to consider :
• The null hypothesis
• p , alpha , and the decision rule,
• Your result. That is, whether the difference in groups, the association, or the correlation is significant or not.
What you should report on your assignments:
• The p -value
• The conclusion, e.g. "There was a significant difference in the mean heights of boys and girls in the class." It is best to preface this with the "reject" or "fail to reject" language concerning your decision about the null hypothesis.
“Size of the effect” / “effect size”
In the context of this book, I use the term "size of the effect" to suggest the use of summary statistics to indicate how large an effect is. This may be, for example the difference in two medians. I try reserve the term “effect size” to refer to the use of effect size statistics. This distinction isn’t necessarily common.
Usually you will consider an effect in relation to the magnitude of measurements. That is, you might look at the difference in medians as a percent of the median of one group or of the global median. Or, you might look at the difference in medians in relation to the range of answers. For example, a one-point difference on a 5-point Likert item. Counts might be expressed as proportions of totals or subsets.
What you should report on assignments :
• The size of the effect. That is, the difference in medians or means, the difference in counts, or the proportions of counts among groups.
• Where appropriate, the size of the effect expressed as a percentage or proportion.
• If there is an effect size statistic—such as r , epsilon -squared, phi , Cramér's V , or Cohen's d —: report this and its interpretation (small, medium, large), and incorporate this into your conclusion.
"Practical" / "Practical importance"
If there is a significant result, the question of practical importance asks if the difference or association is large enough to matter in the real world.
If there is no significant result, the question of practical importance asks if the a difference or association is large enough to warrant another look, for example by running another test with a larger sample size or that controls variability in observations better.
• Your conclusion as to whether this effect is large enough to be important in the real world.
• The context, explanation, or support to justify your conclusion.
• In some cases you might include considerations that aren't included in the data presented. Examples might include the cost of one treatment over another, including time investment, or whether there is a large risk in selecting one treatment over another (e.g., if people's lives are on the line).
A few of xkcd comics
Significant.
xkcd.com/882/
Null hypothesis
xkcd.com/892/
xkcd.com/1478/
Experiments, sampling, and causation
Types of experimental designs, experimental designs.
A true experimental design assigns treatments in a systematic manner. The experimenter must be able to manipulate the experimental treatments and assign them to subjects. Since treatments are randomly assigned to subjects, a causal inference can be made for significant results. That is, we can say that the variation in the dependent variable is caused by the variation in the independent variable.
For interval/ratio data, traditional experimental designs can be analyzed with specific parametric models, assuming other model assumptions are met. These traditional experimental designs include:
• Completely random design
• Randomized complete block design
• Factorial
• Split-plot
• Latin square
Quasi-experiment designs
Often a researcher cannot assign treatments to individual experimental units, but can assign treatments to groups. For example, if students are in a specific grade or class, it would not be practical to randomly assign students to grades or classes. But different classes could receive different treatments (such as different curricula). Causality can be inferred cautiously if treatments are randomly assigned and there is some understanding of the factors that affect the outcome.
Observational studies
In observational studies, the independent variables are not manipulated, and no treatments are assigned. Surveys are often like this, as are studies of natural systems without experimental manipulation. Statistical analysis can reveal the relationships among variables, but causality cannot be inferred. This is because there may be other unstudied variables that affect the measured variables in the study.
Good sampling practices are critical for producing good data. In general, samples need to be collected in a random fashion so that bias is avoided.
In survey data, bias is often introduced by a self-selection bias. For example, internet or telephone surveys include only those who respond to these requests. Might there be some relevant difference in the variables of interest between those who respond to such requests and the general population being surveyed? Or bias could be introduced by the researcher selecting some subset of potential subjects, for example only surveying a 4-H program with particularly cooperative students and ignoring other clubs. This is sometimes called “convenience sampling”.
In election forecasting, good pollsters need to account for selection bias and other biases in the survey process. For example, if a survey is done by landline telephone, those being surveyed are more likely to be older than the general population of voters, and so likely to have a bias in their voting patterns.
Plan ahead and be consistent
It is sometimes necessary to change experimental conditions during the course of an experiment. Equipment might fail, or unusual weather may prevent making meaningful measurements.
But in general, it is much better to plan ahead and be consistent with measurements.
Consistency
People sometimes have the tendency to change measurement frequency or experimental treatments during the course of a study. This inevitably causes headaches in trying to analyze data, and makes writing up the results messy. Try to avoid this.
Controls and checks
If you are testing an experimental treatment, include a check treatment that almost certainly will have an effect and a control treatment that almost certainly won’t. A control treatment will receive no treatment and a check treatment will receive a treatment known to be successful. In an educational setting, perhaps a control group receives no instruction on the topic but on another topic, and the check group will receive standard instruction.
Including checks and controls helps with the analysis in a practical sense, since they serve as standard treatments against which to compare the experimental treatments. In the case where the experimental treatments have similar effects, controls and checks allow you say, for example, “Means for the all experimental treatments were similar, but were higher than the mean for control, and lower than the mean for check treatment.”
Include alternate measurements
It often happens that measuring equipment fails or that a certain measurement doesn’t produce the expected results. It is therefore helpful to include measurements of several variables that can capture the potential effects. Perhaps test scores of students won’t show an effect, but a self-assessment question on how much students learned will.
Include covariates
Including additional independent variables that might affect the dependent variable is often helpful in an analysis. In an educational setting, you might assess student age, grade, school, town, background level in the subject, or how well they are feeling that day.
The effects of covariates on the dependent variable may be of interest in itself. But also, including co-variates in an analysis can better model the data, sometimes making treatment effects more clear or making a model better meet model assumptions.
Optional discussion: Alternative methods to the Null Hypothesis Significance Test
The nhst controversy.
Particularly in the fields of psychology and education, there has been much criticism of the null hypothesis significance test approach. From my reading, the main complaints against NHST tend to be:
• Students and researchers don’t really understand the meaning of p -values.
• p -values don’t include important information like confidence intervals or parameter estimates.
• p -values have properties that may be misleading, for example that they do not represent effect size, and that they change with sample size.
• We often treat an alpha of 0.05 as a magical cutoff value.
Personally, I don’t find these to be very convincing arguments against the NHST approach.
The first complaint is in some sense pedantic: Like so many things, students and researchers learn the definition of p -values at some point and then eventually forget. This doesn’t seem to impact the usefulness of the approach.
The second point has weight only if researchers use only p -values to draw conclusions from statistical tests. As this book points out, one should always consider the size of the effects and practical considerations of the effects, as well present finding in table or graphical form, including confidence intervals or measures of dispersion. There is no reason why parameter estimates, goodness-of-fit statistics, and confidence intervals can’t be included when a NHST approach is followed.
The properties in the third point also don’t count much as criticism if one is using p -values correctly. One should understand that it is possible to have a small effect size and a small p -value, and vice-versa. This is not a problem, because p -values and effect sizes are two different concepts. We shouldn’t expect them to be the same. The fact that p -values change with sample size is also in no way problematic to me. It makes sense that when there is a small effect size or a lot of variability in the data that we need many samples to conclude the effect is likely to be real.
(One case where I think the considerations in the preceding point are commonly problematic is when people use statistical tests to check for the normality or homogeneity of data or model residuals. As sample size increases, these tests are better able to detect small deviations from normality or homoscedasticity. Too many people use them and think their model is inappropriate because the test can detect a small effect size, that is, a small deviation from normality or homoscedasticity).
The fourth point is a good one. It doesn’t make much sense to come to one conclusion if our p -value is 0.049 and the opposite conclusion if our p -value is 0.051. But I think this can be ameliorated by reporting the actual p -values from analyses, and relying less on p -values to evaluate results.
Overall it seems to me that these complaints condemn poor practices that the authors observe: not reporting the size of effects in some manner; not including confidence intervals or measures of dispersion; basing conclusions solely on p -values; and not including important results like parameter estimates and goodness-of-fit statistics.
Alternatives to the NHST approach
Estimates and confidence intervals.
One approach to determining statistical significance is to use estimates and confidence intervals. Estimates could be statistics like means, medians, proportions, or other calculated statistics. This approach can be very straightforward, easy for readers to understand, and easy to present clearly.
Bayesian approach
The most popular competitor to the NHST approach is Bayesian inference. Bayesian inference has the advantage of calculating the probability of the hypothesis given the data , which is what we thought we should be doing in the “Wait, does this make any sense?” section above. Essentially it takes prior knowledge about the distribution of the parameters of interest for a population and adds the information from the measured data to reassess some hypothesis related to the parameters of interest. If the reader will excuse the vagueness of this description, it makes intuitive sense. We start with what we suspect to be the case, and then use new data to assess our hypothesis.
One disadvantage of the Bayesian approach is that it is not obvious in most cases what could be used for legitimate prior information. A second disadvantage is that conducting Bayesian analysis is not as straightforward as the tests presented in this book.
References and further reading
[Video] “Understanding statistical inference” from Statistics Learning Center (Dr. Nic). 2015. www.youtube.com/watch?v=tFRXsngz4UQ .
[Video] “Hypothesis tests, p-value” from Statistics Learning Center (Dr. Nic). 2011. www.youtube.com/watch?v=0zZYBALbZgg .
[Video] “Understanding the p-value” from Statistics Learning Center (Dr. Nic). 2011.
www.youtube.com/watch?v=eyknGvncKLw .
[Video] “Important statistical concepts: significance, strength, association, causation” from Statistics Learning Center (Dr. Nic). 2012. www.youtube.com/watch?v=FG7xnWmZlPE .
“Understanding statistical inference” from Dr. Nic. 2015. Learn and Teach Statistics & Operations Research. creativemaths.net/blog/understanding-statistical-inference/ .
“Basic concepts of hypothesis testing” in McDonald, J.H. 2014. Handbook of Biological Statistics . www.biostathandbook.com/hypothesistesting.html .
“Hypothesis testing” , section 4.3, in Diez, D.M., C.D. Barr , and M. Çetinkaya-Rundel. 2012. OpenIntro Statistics , 2nd ed. www.openintro.org/ .
“Hypothesis Testing with One Sample”, sections 9.1–9.2 in Openstax. 2013. Introductory Statistics . openstax.org/textbooks/introductory-statistics .
"Proving causation" from Dr. Nic. 2013. Learn and Teach Statistics & Operations Research. creativemaths.net/blog/proving-causation/ .
[Video] “Variation and Sampling Error” from Statistics Learning Center (Dr. Nic). 2014. www.youtube.com/watch?v=y3A0lUkpAko .
[Video] “Sampling: Simple Random, Convenience, systematic, cluster, stratified” from Statistics Learning Center (Dr. Nic). 2012. www.youtube.com/watch?v=be9e-Q-jC-0 .
“Confounding variables” in McDonald, J.H. 2014. Handbook of Biological Statistics . www.biostathandbook.com/confounding.html .
“Overview of data collection principles” , section 1.3, in Diez, D.M., C.D. Barr , and M. Çetinkaya-Rundel. 2012. OpenIntro Statistics , 2nd ed. www.openintro.org/ .
“Observational studies and sampling strategies” , section 1.4, in Diez, D.M., C.D. Barr , and M. Çetinkaya-Rundel. 2012. OpenIntro Statistics , 2nd ed. www.openintro.org/ .
“Experiments” , section 1.5, in Diez, D.M., C.D. Barr , and M. Çetinkaya-Rundel. 2012. OpenIntro Statistics , 2nd ed. www.openintro.org/ .
Exercises F
1. Which of the following pair is the null hypothesis?
A) The number of heads from the coin is not different from the number of tails.
B) The number of heads from the coin is different from the number of tails.
2. Which of the following pair is the null hypothesis?
A) The height of boys is different than the height of girls.
B) The height of boys is not different than the height of girls.
3. Which of the following pair is the null hypothesis?
A) There is an association between classroom and sex. That is, there is a difference in counts of girls and boys between the classes.
B) There is no association between classroom and sex. That is, there is no difference in counts of girls and boys between the classes.
4. We flip a coin 10 times and it lands on heads 7 times. We want to know if the coin is fair.
a. What is the null hypothesis?
b. Looking at the code below, and assuming an alpha of 0.05,
What do you decide (use the reject or fail to reject language)?
c. In practical terms, what do you conclude?
binom.test(7, 10, 0.5)
Exact binomial test number of successes = 7, number of trials = 10, p-value = 0.3438
5. We measure the height of 9 boys and 9 girls in a class, in centimeters. We want to know if one group is taller than the other.
c. In practical terms, what do you conclude? Address the practical importance of the results.
Girls = c(152, 150, 140, 160, 145, 155, 150, 152, 147) Boys = c(144, 142, 132, 152, 137, 147, 142, 144, 139) t.test(Girls, Boys)
Welch Two Sample t-test t = 2.9382, df = 16, p-value = 0.009645 mean of x mean of y 150.1111 142.1111
mean(Boys) sd(Boys) quantile(Boys)
mean(Girls) sd(Girls) quantile(Girls) boxplot(cbind(Girls, Boys))
6. We count the number of boys and girls in two classrooms. We are interested to know if there is an association between the classrooms and the number of girls and boys. That is, does the proportion of boys and girls differ statistically across the two classrooms?
Classroom Girls Boys A 13 7 B 5 15
Input =(" Classroom Girls Boys A 13 7 B 5 15 ") Matrix = as.matrix(read.table(textConnection(Input), header=TRUE, row.names=1)) fisher.test(Matrix)
Fisher's Exact Test for Count Data p-value = 0.02484
Matrix rowSums(Matrix) colSums(Matrix) prop.table(Matrix, margin=1) ### Proportions for each row barplot(t(Matrix), beside = TRUE, legend = TRUE, ylim = c(0, 25), xlab = "Class", ylab = "Count")
7. Why should you not rely solely on p -values to make a decision in the real world? (You should have at least two reasons.)
8. Create your own example to show the importance of considering the size of the effect . Describe the scenario: what the research question is, and what kind of data were collected. You may make up data and provide real results, or report hypothetical results.
9. Create your own example to show the importance of weighing other practical considerations . Describe the scenario: what the research question is, what kind of data were collected, what statistical results were reached, and what other practical considerations were brought to bear.
10. What is 5e-4 in common decimal notation?
©2016 by Salvatore S. Mangiafico. Rutgers Cooperative Extension, New Brunswick, NJ.
Non-commercial reproduction of this content, with attribution, is permitted. For-profit reproduction without permission is prohibited.
If you use the code or information in this site in a published work, please cite it as a source. Also, if you are an instructor and use this book in your course, please let me know. My contact information is on the About the Author of this Book page.
Mangiafico, S.S. 2016. Summary and Analysis of Extension Program Evaluation in R, version 1.20.07, revised 2024. rcompanion.org/handbook/ . (Pdf version: rcompanion.org/documents/RHandbookProgramEvaluation.pdf .)
Life With Data
- by bprasad26
How to Use the linearHypothesis() Function in R

The linearHypothesis() function is a valuable statistical tool in R programming. It’s provided in the car package and is used to perform hypothesis testing for a linear model’s coefficients.
To fully grasp the utility of linearHypothesis() , we must understand the basic principles of linear regression and hypothesis testing in the context of model fitting.
Understanding Hypothesis Testing in Regression Analysis
In regression analysis, it’s common to perform hypothesis tests on the model’s coefficients to determine whether the predictors are statistically significant. The null hypothesis asserts that the predictor has no effect on the outcome variable, i.e., its coefficient equals zero. Rejecting the null hypothesis (based on a small p-value, usually less than 0.05) suggests that there’s a statistically significant relationship between the predictor and the outcome variable.
The linearHypothesis( ) Function
linearHypothesis() is a function in R that tests the general linear hypothesis for a model object for which a formula method exists, using a specified test statistic. It allows the user to define a broader set of null hypotheses than just assuming individual coefficients equal to zero.
The linearHypothesis() function can be especially useful for comparing nested models or testing whether a group of variables significantly contributes to the model.
Here’s the basic usage of linearHypothesis() :
In this function:
- model is the model object for which the linear hypothesis is to be tested.
- hypothesis.matrix specifies the null hypotheses.
- rhs is the right-hand side of the linear hypotheses; typically set to 0.
- ... are additional arguments, such as the test argument to specify the type of test statistic to be used (“F” for F-test, “Chisq” for chi-squared test, etc.).
Installing and Loading the Required Package
linearHypothesis() is part of the car package. If you haven’t installed this package yet, you can do so using the following command:
Once installed, load it into your R environment with the library() function:
Using linearHypothesis( ) in Practice
Let’s demonstrate the use of linearHypothesis() with a practical example. We’ll use the mtcars dataset that’s built into R. This dataset comprises various car attributes, and we’ll model miles per gallon (mpg) based on horsepower (hp), weight (wt), and the number of cylinders (cyl).
We first fit a linear model using the lm() function:
Let’s say we want to test the hypothesis that the coefficients for hp and wt are equal to zero. We can set up this hypothesis test using linearHypothesis() :
This command will output the Residual Sum of Squares (RSS) for the model under the null hypothesis, the RSS for the full model, the test statistic, and the p-value for the test. A low p-value suggests that we should reject the null hypothesis.
Using linearHypothesis( ) for Testing Nested Models
linearHypothesis() can also be useful for testing nested models, i.e., comparing a simpler model to a more complex one where the simpler model is a special case of the complex one.
For instance, suppose we want to test if both hp and wt can be dropped from our model without a significant loss of fit. We can formulate this as the null hypothesis that the coefficients for hp and wt are simultaneously zero:
This gives a p-value for the F-test of the hypothesis that these coefficients are zero. If the p-value is small, we reject the null hypothesis and conclude that dropping these predictors from the model would significantly degrade the model fit.
Limitations and Considerations
The linearHypothesis() function is a powerful tool for hypothesis testing in the context of model fitting. However, it’s important to consider the limitations and assumptions of this function. The linearHypothesis() function assumes that the errors of the model are normally distributed and have equal variance. Violations of these assumptions can lead to incorrect results.
As with any statistical function, it’s crucial to have a good understanding of your data and the theory behind the statistical methods you’re using.
The linearHypothesis() function in R is a powerful tool for testing linear hypotheses about a model’s coefficients. This function is very flexible and can be used in various scenarios, including testing the significance of individual predictors and comparing nested models.
Understanding and properly using linearHypothesis() can enhance your data analysis capabilities and help you extract meaningful insights from your data.
Share this:
Leave a reply cancel reply, discover more from life with data.
Subscribe now to keep reading and get access to the full archive.
Type your email…
Continue reading

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

15.5: Hypothesis Tests for Regression Models
- Last updated
- Save as PDF
- Page ID 36197

- Danielle Navarro
- University of New South Wales
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
So far we’ve talked about what a regression model is, how the coefficients of a regression model are estimated, and how we quantify the performance of the model (the last of these, incidentally, is basically our measure of effect size). The next thing we need to talk about is hypothesis tests. There are two different (but related) kinds of hypothesis tests that we need to talk about: those in which we test whether the regression model as a whole is performing significantly better than a null model; and those in which we test whether a particular regression coefficient is significantly different from zero.
At this point, you’re probably groaning internally, thinking that I’m going to introduce a whole new collection of tests. You’re probably sick of hypothesis tests by now, and don’t want to learn any new ones. Me too. I’m so sick of hypothesis tests that I’m going to shamelessly reuse the F-test from Chapter 14 and the t-test from Chapter 13. In fact, all I’m going to do in this section is show you how those tests are imported wholesale into the regression framework.
Testing the model as a whole
Okay, suppose you’ve estimated your regression model. The first hypothesis test you might want to try is one in which the null hypothesis that there is no relationship between the predictors and the outcome, and the alternative hypothesis is that the data are distributed in exactly the way that the regression model predicts . Formally, our “null model” corresponds to the fairly trivial “regression” model in which we include 0 predictors, and only include the intercept term b 0
H 0 :Y i =b 0 +ϵ i
If our regression model has K predictors, the “alternative model” is described using the usual formula for a multiple regression model:
\(H_{1}: Y_{i}=\left(\sum_{k=1}^{K} b_{k} X_{i k}\right)+b_{0}+\epsilon_{i}\)
How can we test these two hypotheses against each other? The trick is to understand that just like we did with ANOVA, it’s possible to divide up the total variance SS tot into the sum of the residual variance SS res and the regression model variance SS mod . I’ll skip over the technicalities, since we covered most of them in the ANOVA chapter, and just note that:
SS mod =SS tot −SS res
And, just like we did with the ANOVA, we can convert the sums of squares in to mean squares by dividing by the degrees of freedom.
\(\mathrm{MS}_{m o d}=\dfrac{\mathrm{SS}_{m o d}}{d f_{m o d}}\) \(\mathrm{MS}_{r e s}=\dfrac{\mathrm{SS}_{r e s}}{d f_{r e s}}\)
So, how many degrees of freedom do we have? As you might expect, the df associated with the model is closely tied to the number of predictors that we’ve included. In fact, it turns out that df mod =K. For the residuals, the total degrees of freedom is df res =N−K−1.
\(\ F={MS_{mod} \over MS_{res}}\)
and the degrees of freedom associated with this are K and N−K−1. This F statistic has exactly the same interpretation as the one we introduced in Chapter 14. Large F values indicate that the null hypothesis is performing poorly in comparison to the alternative hypothesis. And since we already did some tedious “do it the long way” calculations back then, I won’t waste your time repeating them. In a moment I’ll show you how to do the test in R the easy way, but first, let’s have a look at the tests for the individual regression coefficients.
Tests for individual coefficients
The F-test that we’ve just introduced is useful for checking that the model as a whole is performing better than chance. This is important: if your regression model doesn’t produce a significant result for the F-test then you probably don’t have a very good regression model (or, quite possibly, you don’t have very good data). However, while failing this test is a pretty strong indicator that the model has problems, passing the test (i.e., rejecting the null) doesn’t imply that the model is good! Why is that, you might be wondering? The answer to that can be found by looking at the coefficients for the regression.2 model:
I can’t help but notice that the estimated regression coefficient for the baby.sleep variable is tiny (0.01), relative to the value that we get for dan.sleep (-8.95). Given that these two variables are absolutely on the same scale (they’re both measured in “hours slept”), I find this suspicious. In fact, I’m beginning to suspect that it’s really only the amount of sleep that I get that matters in order to predict my grumpiness.
Once again, we can reuse a hypothesis test that we discussed earlier, this time the t-test. The test that we’re interested has a null hypothesis that the true regression coefficient is zero (b=0), which is to be tested against the alternative hypothesis that it isn’t (b≠0). That is:
H 1 : b≠0
How can we test this? Well, if the central limit theorem is kind to us, we might be able to guess that the sampling distribution of \(\ \hat{b}\), the estimated regression coefficient, is a normal distribution with mean centred on b. What that would mean is that if the null hypothesis were true, then the sampling distribution of \(\ \hat{b}\) has mean zero and unknown standard deviation. Assuming that we can come up with a good estimate for the standard error of the regression coefficient, SE (\(\ \hat{b}\)), then we’re in luck. That’s exactly the situation for which we introduced the one-sample t way back in Chapter 13. So let’s define a t-statistic like this,
\(\ t = { \hat{b} \over SE(\hat{b})}\)
I’ll skip over the reasons why, but our degrees of freedom in this case are df=N−K−1. Irritatingly, the estimate of the standard error of the regression coefficient, SE(\(\ \hat{b}\)), is not as easy to calculate as the standard error of the mean that we used for the simpler t-tests in Chapter 13. In fact, the formula is somewhat ugly, and not terribly helpful to look at. For our purposes it’s sufficient to point out that the standard error of the estimated regression coefficient depends on both the predictor and outcome variables, and is somewhat sensitive to violations of the homogeneity of variance assumption (discussed shortly).
In any case, this t-statistic can be interpreted in the same way as the t-statistics that we discussed in Chapter 13. Assuming that you have a two-sided alternative (i.e., you don’t really care if b>0 or b<0), then it’s the extreme values of t (i.e., a lot less than zero or a lot greater than zero) that suggest that you should reject the null hypothesis.
Running the hypothesis tests in R
To compute all of the quantities that we have talked about so far, all you need to do is ask for a summary() of your regression model. Since I’ve been using regression.2 as my example, let’s do that:
The output that this command produces is pretty dense, but we’ve already discussed everything of interest in it, so what I’ll do is go through it line by line. The first line reminds us of what the actual regression model is:
You can see why this is handy, since it was a little while back when we actually created the regression.2 model, and so it’s nice to be reminded of what it was we were doing. The next part provides a quick summary of the residuals (i.e., the ϵi values),
which can be convenient as a quick and dirty check that the model is okay. Remember, we did assume that these residuals were normally distributed, with mean 0. In particular it’s worth quickly checking to see if the median is close to zero, and to see if the first quartile is about the same size as the third quartile. If they look badly off, there’s a good chance that the assumptions of regression are violated. These ones look pretty nice to me, so let’s move on to the interesting stuff. The next part of the R output looks at the coefficients of the regression model:
Each row in this table refers to one of the coefficients in the regression model. The first row is the intercept term, and the later ones look at each of the predictors. The columns give you all of the relevant information. The first column is the actual estimate of b (e.g., 125.96 for the intercept, and -8.9 for the dan.sleep predictor). The second column is the standard error estimate \(\ \hat{\sigma_b}\). The third column gives you the t-statistic, and it’s worth noticing that in this table t= \(\ \hat{b}\) /SE(\(\ \hat{b}\)) every time. Finally, the fourth column gives you the actual p value for each of these tests. 217 The only thing that the table itself doesn’t list is the degrees of freedom used in the t-test, which is always N−K−1 and is listed immediately below, in this line:
The value of df=97 is equal to N−K−1, so that’s what we use for our t-tests. In the final part of the output we have the F-test and the R 2 values which assess the performance of the model as a whole
So in this case, the model performs significantly better than you’d expect by chance (F(2,97)=215.2, p<.001), which isn’t all that surprising: the R 2 =.812 value indicate that the regression model accounts for 81.2% of the variability in the outcome measure. However, when we look back up at the t-tests for each of the individual coefficients, we have pretty strong evidence that the baby.sleep variable has no significant effect; all the work is being done by the dan.sleep variable. Taken together, these results suggest that regression.2 is actually the wrong model for the data: you’d probably be better off dropping the baby.sleep predictor entirely. In other words, the regression.1 model that we started with is the better model.
- Stack Overflow Public questions & answers
- Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
- Talent Build your employer brand
- Advertising Reach developers & technologists worldwide
- Labs The future of collective knowledge sharing
- About the company
Collectives™ on Stack Overflow
Find centralized, trusted content and collaborate around the technologies you use most.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Get early access and see previews of new features.
How to interpret the results of linearHypothesis function when comparing regression coefficients?
I used linearHypothesis function in order to test whether two regression coefficients are significantly different. Do you have any idea how to interpret these results?
Here is my output:
- 1 Pr(>F) is the p-value of the test, and this is the output of interest. You want the interpretation of every output ? – Stéphane Laurent Commented Feb 11, 2019 at 12:40
3 Answers 3
Short Answer
Your F statistic is 104.34 and its p-value 2.2e-16. The corresponding p-value suggests that we can reject the null hypothesis that both coefficients cancel each other at any level of significance commonly used in practice.
Were your p-value greater than 0.05, it is accustomed that you would not reject the null hypothesis.
Long Answer
The linearHypothesis function tests whether the difference between the coefficients is significant. In your example, whether the two betas cancel each other out β1 − β2 = 0.
Linear hypothesis tests are performed using F-statistics. They compare your estimated model against a restrictive model which requires your hypothesis (restriction) to be true.
An alternative linear hypothesis testing would be to test whether β1 or β2 are nonzero, so we jointly test the hypothesis β1=0 and β2 = 0 rather than testing each one at a time. Here the null is rejected when one is rejected. Rejection here means that at least one of your hypotheses can be rejected. In other words provide both linear restrictions to be tested as strings
Here are few examples of the multitude of ways you can test hypothese:
You can test a linear combination of coeffecients
joint probability
Aside from the t statistics, which test for the predictive power of each variable in the presence of all the others, another test which can be used is the F-test. (this is the F-test that you would get at the bottom of a linear model)
This tests the null hypothesis that all of the β’s are equal to zero against the alternative that allows them to take any values. If we reject this null hypothesis (which we do because the p-value is small), then this is the same as saying there is enough evidence to conclude that at least one of the covariates has predictive power in our linear model, i.e. that using a regression is predictively ‘better’ than just guessing the average.
So basically, you are testing whether all coefficients are different from zero or some other arbitrary linear hypothesis, as opposed to a t-test where you are testing individual coefficients.
The answer given above is detailed enough except that for this test we are more interested in the two variables hence the linear hypothesis does not investigate the null hypothesis that all of the β’s are equal to zero against the alternative that allows them to take any values but just for two variables of interest which makes this test equivalent to a t-test.
- 1 As it’s currently written, your answer is unclear. Please edit to add additional details that will help others understand how this addresses the question asked. You can find more information on how to write good answers in the help center . – Community Bot Commented Sep 14, 2022 at 19:22
Your Answer
Reminder: Answers generated by artificial intelligence tools are not allowed on Stack Overflow. Learn more
Sign up or log in
Post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged r regression or ask your own question .
- Featured on Meta
- Upcoming sign-up experiments related to tags
- Policy: Generative AI (e.g., ChatGPT) is banned
- The return of Staging Ground to Stack Overflow
- The 2024 Developer Survey Is Live
Hot Network Questions
- Going around in circles
- Why should you want to use a smaller size control group?
- 2D Pathfinding with rope constraint
- Approximation algorithm for binary (linear) programs
- To whom did the neogrammarians react?
- The term 'sfp' is not recognized
- What was the Nuclear Boy Scout's Eagle Scout Project?
- Check if license plate number is formatted correctly
- Can you perform harmonics on wine glasses?
- Is it grammatically correct to say 'I suspect this clause to be a bit sloppy English'?
- Does it matter to de-select faces before going back to Object Mode?
- Hydrogen in Organometallic Chemistry
- Does the Cardinal Supremum Commute with the Cardinal Power?
- Why do some op amps' datasheet specify phase margin at open loop?
- Trying to use 'Equations'
- Nonconsecutive Anti-Knight Fillomino?
- Best practices for relicensing what was once a derivative work
- Is there a maximum amount of time I should spend on an exercise bike?
- How to create a galvanized pipe with a twist?
- Probably a nit: "openssl x509" displays the serial number sometimes as octet string, sometimes as integer
- Is intrinsic spin a quantum or/and a relativistic phenomenon?
- Why are amber bottles used to store Water for HPLC?
- How do regression loss functions like MAE and MSE work although they remove the plus/minus sign?
- Why are heavy metals toxic? Lead and Carbon are in the same group. One is toxic, the other is not
| linearHypothesis {car} | R Documentation |
Test Linear Hypothesis
Description.
Generic function for testing a linear hypothesis, and methods for linear models, generalized linear models, multivariate linear models, linear and generalized linear mixed-effects models, generalized linear models fit with svyglm in the survey package, robust linear models fit with rlm in the MASS package, and other models that have methods for coef and vcov . For mixed-effects models, the tests are Wald chi-square tests for the fixed effects.
| fitted model object. The default method of works for models for which the estimated parameters can be retrieved by and the corresponding estimated covariance matrix by . See the for more information. | |
| matrix (or vector) giving linear combinations of coefficients by rows, or a character vector giving the hypothesis in symbolic form (see ). | |
| right-hand-side vector for hypothesis, with as many entries as rows in the hypothesis matrix; can be omitted, in which case it defaults to a vector of zeroes. For a multivariate linear model, is a matrix, defaulting to 0. This argument isn't available for F-tests for linear mixed models. | |
| if (the default), a model with aliased coefficients produces an error; if , the aliased coefficients are ignored, and the hypothesis matrix should not have columns for them. For a multivariate linear model: will return the hypothesis and error SSP matrices even if the latter is singular; useful for computing univariate repeated-measures ANOVAs where there are fewer subjects than df for within-subject effects. | |
| For the method, if an F-test is requested and if is missing, the error degrees of freedom will be computed by applying the function to the model; if returns or , then a chi-square test will be substituted for the F-test (with a message to that effect. | |
| an optional data frame giving a factor or factors defining the intra-subject model for multivariate repeated-measures data. See for an explanation of the intra-subject design and for further explanation of the other arguments relating to intra-subject factors. | |
| names of contrast-generating functions to be applied by default to factors and ordered factors, respectively, in the within-subject “data”; the contrasts must produce an intra-subject model matrix in which different terms are orthogonal. | |
| a one-sided model formula using the “data” in and specifying the intra-subject design. | |
| the quoted name of a term, or a vector of quoted names of terms, in the intra-subject design to be tested. | |
| check that columns of the intra-subject model matrix for different terms are mutually orthogonal (default, ). Set to only if you have checked that the intra-subject model matrix is block-orthogonal. | |
| transformation matrix to be applied to the repeated measures in multivariate repeated-measures data; if no intra-subject model is specified, no response-transformation is applied; if an intra-subject model is specified via the , , and (optionally) arguments, then is generated automatically from the argument. | |
| in method for objects: optional error sum-of-squares-and-products matrix; if missing, it is computed from the model. In method for objects: if , print the sum-of-squares and cross-products matrix for error. | |
| character string, or , specifying whether to compute the finite-sample F statistic (with approximate F distribution) or the large-sample Chi-squared statistic (with asymptotic Chi-squared distribution). For a multivariate linear model, the multivariate test statistic to report — one or more of , , , or , with as the default. | |
| an optional character string to label the output. | |
| inverse of sum of squares and products of the model matrix; if missing it is computed from the model. | |
| a function for estimating the covariance matrix of the regression coefficients, e.g., , or an estimated covariance matrix for . See also . For the and methods, must be a function (defaulting to ) to be applied to each model in the list. | |
| a vector of coefficient estimates. The default is to get the coefficient estimates from the argument, but the user can input any vector of the correct length. For the and methods, must be a function (defaulting to ) to be applied to each model in the list. | |
| logical or character. Convenience interface to (instead of using the argument ). Can be set either to a character value specifying the argument of or , in which case is used implicitly. The default is . | |
| If , the hypothesis matrix, right-hand-side vector (or matrix), and estimated value of the hypothesis are printed to standard output; if (the default), the hypothesis is only printed in symbolic form and the value of the hypothesis is not printed. | |
| an object produced by . | |
| if (the default), print the sum-of-squares and cross-products matrix for the hypothesis and the response-transformation matrix. | |
| minimum number of signficiant digits to print. | |
| a to be matched against coefficient names. | |
| for internal use by methods that call the default method. | |
| arguments to pass down. |
linearHypothesis computes either a finite-sample F statistic or asymptotic Chi-squared statistic for carrying out a Wald-test-based comparison between a model and a linearly restricted model. The default method will work with any model object for which the coefficient vector can be retrieved by coef and the coefficient-covariance matrix by vcov (otherwise the argument vcov. has to be set explicitly). For computing the F statistic (but not the Chi-squared statistic) a df.residual method needs to be available. If a formula method exists, it is used for pretty printing.
The method for "lm" objects calls the default method, but it changes the default test to "F" , supports the convenience argument white.adjust (for backwards compatibility), and enhances the output by the residual sums of squares. For "glm" objects just the default method is called (bypassing the "lm" method). The "svyglm" method also calls the default method.
Multinomial logit models fit by the multinom function in the nnet package invoke the default method, and the coefficient names are composed from the response-level names and conventional coefficient names, separated by a period ( "." ): see one of the examples below.
The function lht also dispatches to linearHypothesis .
The hypothesis matrix can be supplied as a numeric matrix (or vector), the rows of which specify linear combinations of the model coefficients, which are tested equal to the corresponding entries in the right-hand-side vector, which defaults to a vector of zeroes.
Alternatively, the hypothesis can be specified symbolically as a character vector with one or more elements, each of which gives either a linear combination of coefficients, or a linear equation in the coefficients (i.e., with both a left and right side separated by an equals sign). Components of a linear expression or linear equation can consist of numeric constants, or numeric constants multiplying coefficient names (in which case the number precedes the coefficient, and may be separated from it by spaces or an asterisk); constants of 1 or -1 may be omitted. Spaces are always optional. Components are separated by plus or minus signs. Newlines or tabs in hypotheses will be treated as spaces. See the examples below.
If the user sets the arguments coef. and vcov. , then the computations are done without reference to the model argument. This is like assuming that coef. is normally distibuted with estimated variance vcov. and the linearHypothesis will compute tests on the mean vector for coef. , without actually using the model argument.
A linear hypothesis for a multivariate linear model (i.e., an object of class "mlm" ) can optionally include an intra-subject transformation matrix for a repeated-measures design. If the intra-subject transformation is absent (the default), the multivariate test concerns all of the corresponding coefficients for the response variables. There are two ways to specify the transformation matrix for the repeated measures:
The transformation matrix can be specified directly via the P argument.
A data frame can be provided defining the repeated-measures factor or factors via idata , with default contrasts given by the icontrasts argument. An intra-subject model-matrix is generated from the one-sided formula specified by the idesign argument; columns of the model matrix corresponding to different terms in the intra-subject model must be orthogonal (as is insured by the default contrasts). Note that the contrasts given in icontrasts can be overridden by assigning specific contrasts to the factors in idata . The repeated-measures transformation matrix consists of the columns of the intra-subject model matrix corresponding to the term or terms in iterms . In most instances, this will be the simpler approach, and indeed, most tests of interests can be generated automatically via the Anova function.
matchCoefs is a convenience function that can sometimes help in formulating hypotheses; for example matchCoefs(mod, ":") will return the names of all interaction coefficients in the model mod .
For a univariate model, an object of class "anova" which contains the residual degrees of freedom in the model, the difference in degrees of freedom, Wald statistic (either "F" or "Chisq" ), and corresponding p value. The value of the linear hypothesis and its covariance matrix are returned respectively as "value" and "vcov" attributes of the object (but not printed).
For a multivariate linear model, an object of class "linearHypothesis.mlm" , which contains sums-of-squares-and-product matrices for the hypothesis and for error, degrees of freedom for the hypothesis and error, and some other information.
The returned object normally would be printed.
Achim Zeileis and John Fox [email protected]
Fox, J. (2016) Applied Regression Analysis and Generalized Linear Models , Third Edition. Sage.
Fox, J. and Weisberg, S. (2019) An R Companion to Applied Regression , Third Edition, Sage.
Hand, D. J., and Taylor, C. C. (1987) Multivariate Analysis of Variance and Repeated Measures: A Practical Approach for Behavioural Scientists. Chapman and Hall.
O'Brien, R. G., and Kaiser, M. K. (1985) MANOVA method for analyzing repeated measures designs: An extensive primer. Psychological Bulletin 97 , 316–333.
anova , Anova , waldtest , hccm , vcovHC , vcovHAC , coef , vcov
lineartestr
The goal of lineartestr is to contrast the linear hypothesis of a model:
Using the Domínguez-Lobato test which relies on wild-bootstrap. Also the Ramsey RESET test is implemented.
Installation
You can install the released version of lineartestr from CRAN with:
And the development version from GitHub with:
- Manuel A. Domínguez and Ignacio N. Lobato (2019). Specification testing with estimated variables. Econometric Reviews.
- Garza F (2020). lineartestr: Test the linear specification of a model . R package version 1.0.0, https://github.com/FedericoGarza/lineartestr .
Simplest linear models using lm function
Also lineartestr can plot the results
Run in parallel !
Reset test can also be used to test the linear hypothesis.
An then we can plot the results
Linear fixed effects with lfe
Arma models, monthly downloads, pull requests, last published, functions in lineartestr (1.0.0).
car Companion to Applied Regression
- Using car functions inside user functions
- Anova: Anova Tables for Various Statistical Models
- avPlots: Added-Variable Plots
- bcPower: Box-Cox, Box-Cox with Negatives Allowed, Yeo-Johnson and...
- Boot: Bootstrapping for regression models
- boxCox: Graph the profile log-likelihood for Box-Cox transformations...
- boxCoxVariable: Constructed Variable for Box-Cox Transformation
- Boxplot: Boxplots With Point Identification
- boxTidwell: Box-Tidwell Transformations
- brief: Print Abbreviated Ouput
- car-defunct: Defunct Functions in the car Package
- car-deprecated: Deprecated Functions in the car Package
- carHexsticker: View the Official Hex Sticker for the car Package
- car-internal: Internal Objects for the 'car' package
- carPalette: Set or Retrieve 'car' Package Color Palette
- carWeb: Access to the R Companion to Applied Regression Website
- ceresPlots: Ceres Plots
- compareCoefs: Print estimated coefficients and their standard errors in a...
- Contrasts: Functions to Construct Contrasts
- crPlots: Component+Residual (Partial Residual) Plots
- deltaMethod: Estimate and Standard Error of a Nonlinear Function of...
- densityPlot: Nonparametric Density Estimates
- dfbetaPlots: dfbeta and dfbetas Index Plots
- durbinWatsonTest: Durbin-Watson Test for Autocorrelated Errors
- Ellipses: Ellipses, Data Ellipses, and Confidence Ellipses
- Export: Export a data frame to disk in one of many formats
- hccm: Heteroscedasticity-Corrected Covariance Matrices
- hist.boot: Methods Functions to Support 'boot' Objects
- Import: Import data from many file formats
- infIndexPlot: Influence Index Plot
- influence-mixed-models: Influence Diagnostics for Mixed-Effects Models
- influencePlot: Regression Influence Plot
- invResPlot: Inverse Response Plots to Transform the Response
- invTranPlot: Choose a Predictor Transformation Visually or Numerically
- leveneTest: Levene's Test
- leveragePlots: Regression Leverage Plots
- linearHypothesis: Test Linear Hypothesis
- logit: Logit Transformation
- marginalModelPlot: Marginal Model Plotting
- mcPlots: Draw Linear Model Marginal and Conditional Plots in Parallel...
- ncvTest: Score Test for Non-Constant Error Variance
- outlierTest: Bonferroni Outlier Test
- panel.car: Panel Function for Coplots
- pointLabel: Label placement for points to avoid overlaps
- poTest: Test for Proportional Odds in the Proportional-Odds...
- powerTransform: Finding Univariate or Multivariate Power Transformations
- Predict: Model Predictions
- qqPlot: Quantile-Comparison Plot
- recode: Recode a Variable
- regLine: Plot Regression Line
- residualPlots: Residual Plots for Linear and Generalized Linear Models
- Browse all...
linearHypothesis : Test Linear Hypothesis In car: Companion to Applied Regression
| linearHypothesis | R Documentation |
Test Linear Hypothesis
Description.
Generic function for testing a linear hypothesis, and methods for linear models, generalized linear models, multivariate linear models, linear and generalized linear mixed-effects models, generalized linear models fit with svyglm in the survey package, robust linear models fit with rlm in the MASS package, and other models that have methods for coef and vcov . For mixed-effects models, the tests are Wald chi-square tests for the fixed effects.
| fitted model object. The default method of works for models for which the estimated parameters can be retrieved by and the corresponding estimated covariance matrix by . See the for more information. | |
| matrix (or vector) giving linear combinations of coefficients by rows, or a character vector giving the hypothesis in symbolic form (see ). | |
| right-hand-side vector for hypothesis, with as many entries as rows in the hypothesis matrix; can be omitted, in which case it defaults to a vector of zeroes. For a multivariate linear model, is a matrix, defaulting to 0. This argument isn't available for F-tests for linear mixed models. | |
| if (the default), a model with aliased coefficients produces an error; if , the aliased coefficients are ignored, and the hypothesis matrix should not have columns for them. For a multivariate linear model: will return the hypothesis and error SSP matrices even if the latter is singular; useful for computing univariate repeated-measures ANOVAs where there are fewer subjects than df for within-subject effects. | |
| For the method, if an F-test is requested and if is missing, the error degrees of freedom will be computed by applying the function to the model; if returns or , then a chi-square test will be substituted for the F-test (with a message to that effect. | |
| an optional data frame giving a factor or factors defining the intra-subject model for multivariate repeated-measures data. See for an explanation of the intra-subject design and for further explanation of the other arguments relating to intra-subject factors. | |
| names of contrast-generating functions to be applied by default to factors and ordered factors, respectively, in the within-subject “data”; the contrasts must produce an intra-subject model matrix in which different terms are orthogonal. | |
| a one-sided model formula using the “data” in and specifying the intra-subject design. | |
| the quoted name of a term, or a vector of quoted names of terms, in the intra-subject design to be tested. | |
| check that columns of the intra-subject model matrix for different terms are mutually orthogonal (default, ). Set to only if you have checked that the intra-subject model matrix is block-orthogonal. | |
| transformation matrix to be applied to the repeated measures in multivariate repeated-measures data; if no intra-subject model is specified, no response-transformation is applied; if an intra-subject model is specified via the , , and (optionally) arguments, then is generated automatically from the argument. | |
| in method for objects: optional error sum-of-squares-and-products matrix; if missing, it is computed from the model. In method for objects: if , print the sum-of-squares and cross-products matrix for error. | |
| character string, or , specifying whether to compute the finite-sample F statistic (with approximate F distribution) or the large-sample Chi-squared statistic (with asymptotic Chi-squared distribution). For a multivariate linear model, the multivariate test statistic to report — one or more of , , , or , with as the default. | |
| an optional character string to label the output. | |
| inverse of sum of squares and products of the model matrix; if missing it is computed from the model. | |
| a function for estimating the covariance matrix of the regression coefficients, e.g., , or an estimated covariance matrix for . See also . For the and methods, must be a function (defaulting to ) to be applied to each model in the list. | |
| a vector of coefficient estimates. The default is to get the coefficient estimates from the argument, but the user can input any vector of the correct length. For the and methods, must be a function (defaulting to ) to be applied to each model in the list. | |
| logical or character. Convenience interface to (instead of using the argument ). Can be set either to a character value specifying the argument of or , in which case is used implicitly. The default is . | |
| If , the hypothesis matrix, right-hand-side vector (or matrix), and estimated value of the hypothesis are printed to standard output; if (the default), the hypothesis is only printed in symbolic form and the value of the hypothesis is not printed. | |
| an object produced by . | |
| if (the default), print the sum-of-squares and cross-products matrix for the hypothesis and the response-transformation matrix. | |
| minimum number of signficiant digits to print. | |
| a regular expression to be matched against coefficient names. | |
| for internal use by methods that call the default method. | |
| arguments to pass down. |
linearHypothesis computes either a finite-sample F statistic or asymptotic Chi-squared statistic for carrying out a Wald-test-based comparison between a model and a linearly restricted model. The default method will work with any model object for which the coefficient vector can be retrieved by coef and the coefficient-covariance matrix by vcov (otherwise the argument vcov. has to be set explicitly). For computing the F statistic (but not the Chi-squared statistic) a df.residual method needs to be available. If a formula method exists, it is used for pretty printing.
The method for "lm" objects calls the default method, but it changes the default test to "F" , supports the convenience argument white.adjust (for backwards compatibility), and enhances the output by the residual sums of squares. For "glm" objects just the default method is called (bypassing the "lm" method). The "svyglm" method also calls the default method.
Multinomial logit models fit by the multinom function in the nnet package invoke the default method, and the coefficient names are composed from the response-level names and conventional coefficient names, separated by a period ( "." ): see one of the examples below.
The function lht also dispatches to linearHypothesis .
The hypothesis matrix can be supplied as a numeric matrix (or vector), the rows of which specify linear combinations of the model coefficients, which are tested equal to the corresponding entries in the right-hand-side vector, which defaults to a vector of zeroes.
Alternatively, the hypothesis can be specified symbolically as a character vector with one or more elements, each of which gives either a linear combination of coefficients, or a linear equation in the coefficients (i.e., with both a left and right side separated by an equals sign). Components of a linear expression or linear equation can consist of numeric constants, or numeric constants multiplying coefficient names (in which case the number precedes the coefficient, and may be separated from it by spaces or an asterisk); constants of 1 or -1 may be omitted. Spaces are always optional. Components are separated by plus or minus signs. Newlines or tabs in hypotheses will be treated as spaces. See the examples below.
If the user sets the arguments coef. and vcov. , then the computations are done without reference to the model argument. This is like assuming that coef. is normally distibuted with estimated variance vcov. and the linearHypothesis will compute tests on the mean vector for coef. , without actually using the model argument.
A linear hypothesis for a multivariate linear model (i.e., an object of class "mlm" ) can optionally include an intra-subject transformation matrix for a repeated-measures design. If the intra-subject transformation is absent (the default), the multivariate test concerns all of the corresponding coefficients for the response variables. There are two ways to specify the transformation matrix for the repeated measures:
The transformation matrix can be specified directly via the P argument.
A data frame can be provided defining the repeated-measures factor or factors via idata , with default contrasts given by the icontrasts argument. An intra-subject model-matrix is generated from the one-sided formula specified by the idesign argument; columns of the model matrix corresponding to different terms in the intra-subject model must be orthogonal (as is insured by the default contrasts). Note that the contrasts given in icontrasts can be overridden by assigning specific contrasts to the factors in idata . The repeated-measures transformation matrix consists of the columns of the intra-subject model matrix corresponding to the term or terms in iterms . In most instances, this will be the simpler approach, and indeed, most tests of interests can be generated automatically via the Anova function.
matchCoefs is a convenience function that can sometimes help in formulating hypotheses; for example matchCoefs(mod, ":") will return the names of all interaction coefficients in the model mod .
For a univariate model, an object of class "anova" which contains the residual degrees of freedom in the model, the difference in degrees of freedom, Wald statistic (either "F" or "Chisq" ), and corresponding p value. The value of the linear hypothesis and its covariance matrix are returned respectively as "value" and "vcov" attributes of the object (but not printed).
For a multivariate linear model, an object of class "linearHypothesis.mlm" , which contains sums-of-squares-and-product matrices for the hypothesis and for error, degrees of freedom for the hypothesis and error, and some other information.
The returned object normally would be printed.
Achim Zeileis and John Fox [email protected]
Fox, J. (2016) Applied Regression Analysis and Generalized Linear Models , Third Edition. Sage.
Fox, J. and Weisberg, S. (2019) An R Companion to Applied Regression , Third Edition, Sage.
Hand, D. J., and Taylor, C. C. (1987) Multivariate Analysis of Variance and Repeated Measures: A Practical Approach for Behavioural Scientists. Chapman and Hall.
O'Brien, R. G., and Kaiser, M. K. (1985) MANOVA method for analyzing repeated measures designs: An extensive primer. Psychological Bulletin 97 , 316–333.
anova , Anova , waldtest , hccm , vcovHC , vcovHAC , coef , vcov
Related to linearHypothesis in car ...
R package documentation, browse r packages, we want your feedback.

Add the following code to your website.
REMOVE THIS Copy to clipboard
For more information on customizing the embed code, read Embedding Snippets .
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Linear Regression in R | A Step-by-Step Guide & Examples
Linear Regression in R | A Step-by-Step Guide & Examples
Published on February 25, 2020 by Rebecca Bevans . Revised on May 10, 2024.
Linear regression is a regression model that uses a straight line to describe the relationship between variables . It finds the line of best fit through your data by searching for the value of the regression coefficient(s) that minimizes the total error of the model.
There are two main types of linear regression:
- Simple linear regression uses only one independent variable
- Multiple linear regression uses two or more independent variables
In this step-by-step guide, we will walk you through linear regression in R using two sample datasets.
Download the sample datasets to try it yourself.
Simple regression dataset Multiple regression dataset
Table of contents
Getting started in r, step 1: load the data into r, step 2: make sure your data meet the assumptions, step 3: perform the linear regression analysis, step 4: check for homoscedasticity, step 5: visualize the results with a graph, step 6: report your results, other interesting articles.
Start by downloading R and RStudio . Then open RStudio and click on File > New File > R Script .
As we go through each step , you can copy and paste the code from the text boxes directly into your script. To run the code, highlight the lines you want to run and click on the Run button on the top right of the text editor (or press ctrl + enter on the keyboard).
To install the packages you need for the analysis, run this code (you only need to do this once):
Next, load the packages into your R environment by running this code (you need to do this every time you restart R):
Prevent plagiarism. Run a free check.
Follow these four steps for each dataset:
- In RStudio, go to File > Import dataset > From Text (base) .
- Choose the data file you have downloaded ( income.data or heart.data ), and an Import Dataset window pops up.
- In the Data Frame window, you should see an X (index) column and columns listing the data for each of the variables ( income and happiness or biking , smoking , and heart.disease ).
- Click on the Import button and the file should appear in your Environment tab on the upper right side of the RStudio screen.
After you’ve loaded the data, check that it has been read in correctly using summary() .
Simple regression
Because both our variables are quantitative , when we run this function we see a table in our console with a numeric summary of the data. This tells us the minimum, median , mean , and maximum values of the independent variable (income) and dependent variable (happiness):
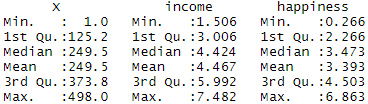
Multiple regression
Again, because the variables are quantitative, running the code produces a numeric summary of the data for the independent variables (smoking and biking) and the dependent variable (heart disease):

We can use R to check that our data meet the four main assumptions for linear regression .
- Independence of observations (aka no autocorrelation)
Because we only have one independent variable and one dependent variable, we don’t need to test for any hidden relationships among variables.
If you know that you have autocorrelation within variables (i.e. multiple observations of the same test subject), then do not proceed with a simple linear regression! Use a structured model, like a linear mixed-effects model, instead.
To check whether the dependent variable follows a normal distribution , use the hist() function.
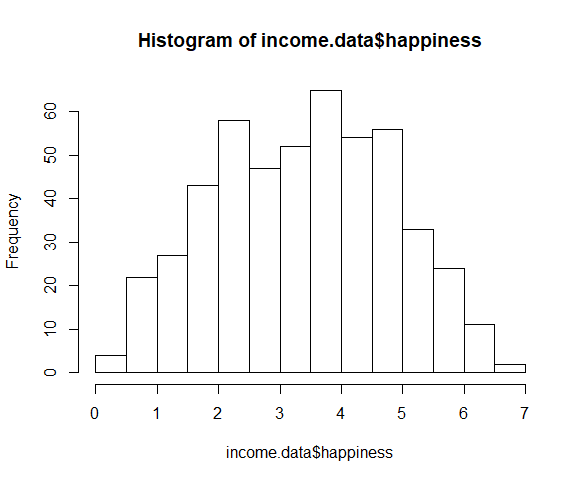
The observations are roughly bell-shaped (more observations in the middle of the distribution, fewer on the tails), so we can proceed with the linear regression.
The relationship between the independent and dependent variable must be linear. We can test this visually with a scatter plot to see if the distribution of data points could be described with a straight line.
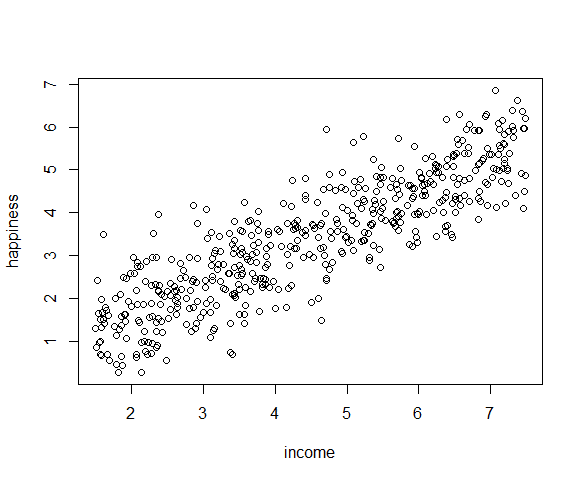
The relationship looks roughly linear, so we can proceed with the linear model.
- Homoscedasticity (aka homogeneity of variance )
This means that the prediction error doesn’t change significantly over the range of prediction of the model. We can test this assumption later, after fitting the linear model.
Use the cor() function to test the relationship between your independent variables and make sure they aren’t too highly correlated.
When we run this code, the output is 0.015. The correlation between biking and smoking is small (0.015 is only a 1.5% correlation), so we can include both parameters in our model.
Use the hist() function to test whether your dependent variable follows a normal distribution .
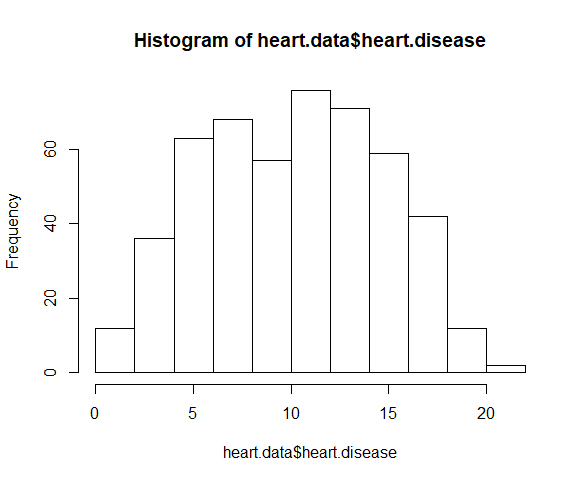
The distribution of observations is roughly bell-shaped, so we can proceed with the linear regression.
We can check this using two scatterplots: one for biking and heart disease, and one for smoking and heart disease.
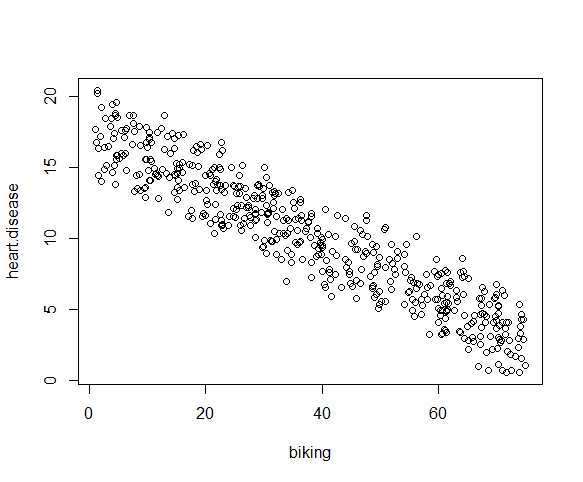
Although the relationship between smoking and heart disease is a bit less clear, it still appears linear. We can proceed with linear regression.
- Homoscedasticity
We will check this after we make the model.
Now that you’ve determined your data meet the assumptions, you can perform a linear regression analysis to evaluate the relationship between the independent and dependent variables.
Simple regression: income and happiness
Let’s see if there’s a linear relationship between income and happiness in our survey of 500 people with incomes ranging from $15k to $75k, where happiness is measured on a scale of 1 to 10.
To perform a simple linear regression analysis and check the results, you need to run two lines of code. The first line of code makes the linear model, and the second line prints out the summary of the model:
The output looks like this:
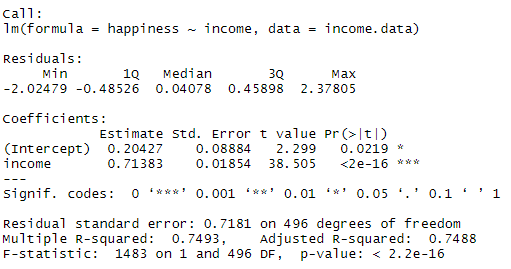
This output table first presents the model equation, then summarizes the model residuals (see step 4).
The Coefficients section shows:
- The estimates ( Estimate ) for the model parameters – the value of the y-intercept (in this case 0.204) and the estimated effect of income on happiness (0.713).
- The standard error of the estimated values ( Std. Error ).
- The test statistic ( t value , in this case the t statistic ).
- The p value ( Pr(>| t | ) ), aka the probability of finding the given t statistic if the null hypothesis of no relationship were true.
The final three lines are model diagnostics – the most important thing to note is the p value (here it is 2.2e-16, or almost zero), which will indicate whether the model fits the data well.
From these results, we can say that there is a significant positive relationship between income and happiness ( p value < 0.001), with a 0.713-unit (+/- 0.01) increase in happiness for every unit increase in income.
Multiple regression: biking, smoking, and heart disease
Let’s see if there’s a linear relationship between biking to work, smoking, and heart disease in our imaginary survey of 500 towns. The rates of biking to work range between 1 and 75%, rates of smoking between 0.5 and 30%, and rates of heart disease between 0.5% and 20.5%.
To test the relationship, we first fit a linear model with heart disease as the dependent variable and biking and smoking as the independent variables. Run these two lines of code:
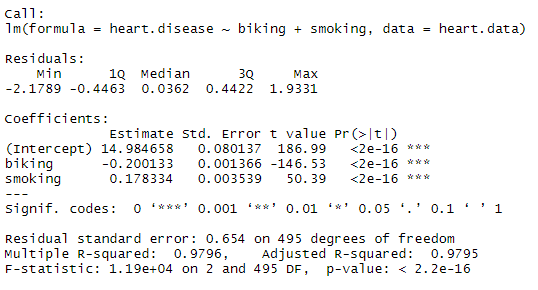
The estimated effect of biking on heart disease is -0.2, while the estimated effect of smoking is 0.178.
This means that for every 1% increase in biking to work, there is a correlated 0.2% decrease in the incidence of heart disease. Meanwhile, for every 1% increase in smoking, there is a 0.178% increase in the rate of heart disease.
The standard errors for these regression coefficients are very small, and the t statistics are very large (-147 and 50.4, respectively). The p values reflect these small errors and large t statistics. For both parameters, there is almost zero probability that this effect is due to chance.
Remember that these data are made up for this example, so in real life these relationships would not be nearly so clear!
Before proceeding with data visualization, we should make sure that our models fit the homoscedasticity assumption of the linear model.
We can run plot(income.happiness.lm) to check whether the observed data meets our model assumptions:
Note that the par(mfrow()) command will divide the Plots window into the number of rows and columns specified in the brackets. So par(mfrow=c(2,2)) divides it up into two rows and two columns. To go back to plotting one graph in the entire window, set the parameters again and replace the (2,2) with (1,1).
These are the residual plots produced by the code:
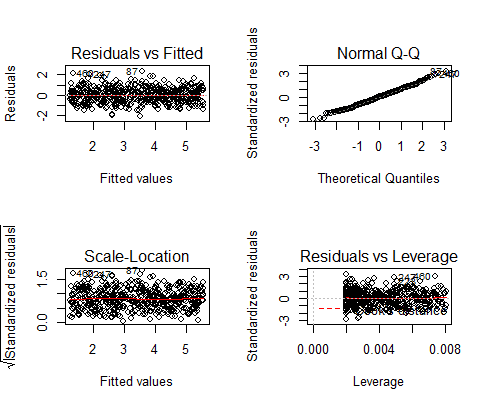
Residuals are the unexplained variance . They are not exactly the same as model error, but they are calculated from it, so seeing a bias in the residuals would also indicate a bias in the error.
The most important thing to look for is that the red lines representing the mean of the residuals are all basically horizontal and centered around zero. This means there are no outliers or biases in the data that would make a linear regression invalid.
In the Normal Q-Qplot in the top right, we can see that the real residuals from our model form an almost perfectly one-to-one line with the theoretical residuals from a perfect model.
Based on these residuals, we can say that our model meets the assumption of homoscedasticity.
Again, we should check that our model is actually a good fit for the data, and that we don’t have large variation in the model error, by running this code:
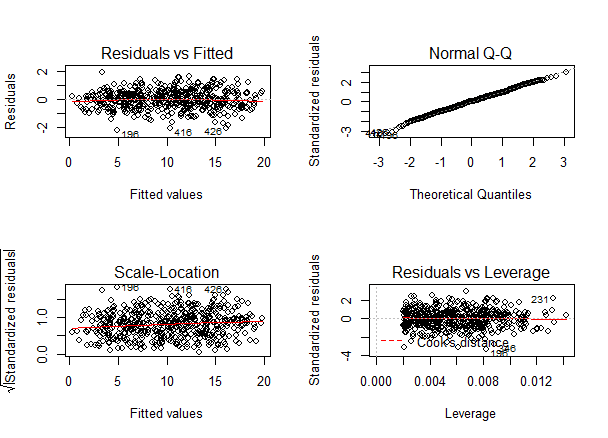
As with our simple regression, the residuals show no bias, so we can say our model fits the assumption of homoscedasticity.
Next, we can plot the data and the regression line from our linear regression model so that the results can be shared.
Follow 4 steps to visualize the results of your simple linear regression.
- Plot the data points on a graph
- Add the linear regression line to the plotted data
Add the regression line using geom_smooth() and typing in lm as your method for creating the line. This will add the line of the linear regression as well as the standard error of the estimate (in this case +/- 0.01) as a light grey stripe surrounding the line:
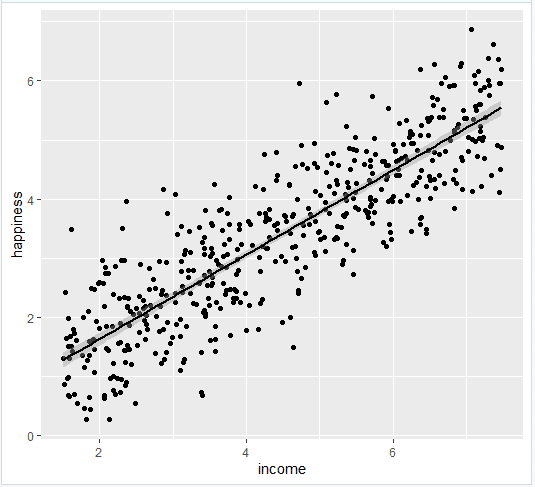
- Add the equation for the regression line.
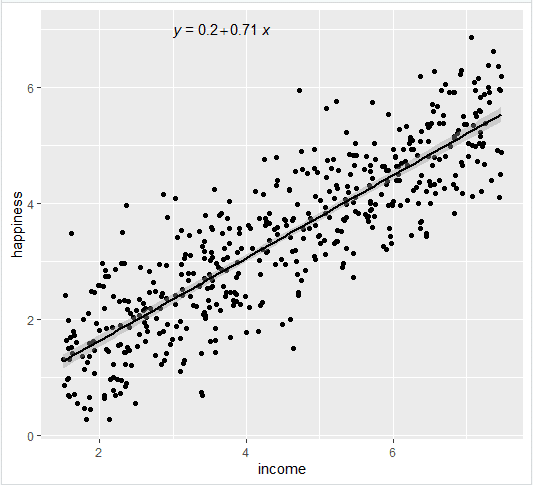
- Make the graph ready for publication
We can add some style parameters using theme_bw() and making custom labels using labs() .
This produces the finished graph that you can include in your papers:
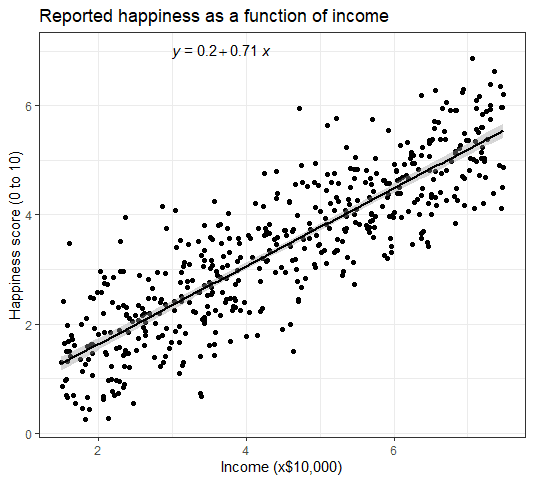
The visualization step for multiple regression is more difficult than for simple regression, because we now have two predictors. One option is to plot a plane, but these are difficult to read and not often published.
We will try a different method: plotting the relationship between biking and heart disease at different levels of smoking. In this example, smoking will be treated as a factor with three levels, just for the purposes of displaying the relationships in our data.
There are 7 steps to follow.
- Create a new dataframe with the information needed to plot the model
Use the function expand.grid() to create a dataframe with the parameters you supply. Within this function we will:
- Create a sequence from the lowest to the highest value of your observed biking data;
- Choose the minimum, mean, and maximum values of smoking, in order to make 3 levels of smoking over which to predict rates of heart disease.
This will not create anything new in your console, but you should see a new data frame appear in the Environment tab. Click on it to view it.
- Predict the values of heart disease based on your linear model
Next we will save our ‘predicted y’ values as a new column in the dataset we just created.
- Round the smoking numbers to two decimals
This will make the legend easier to read later on.
- Change the ‘smoking’ variable into a factor
This allows us to plot the interaction between biking and heart disease at each of the three levels of smoking we chose.
- Plot the original data
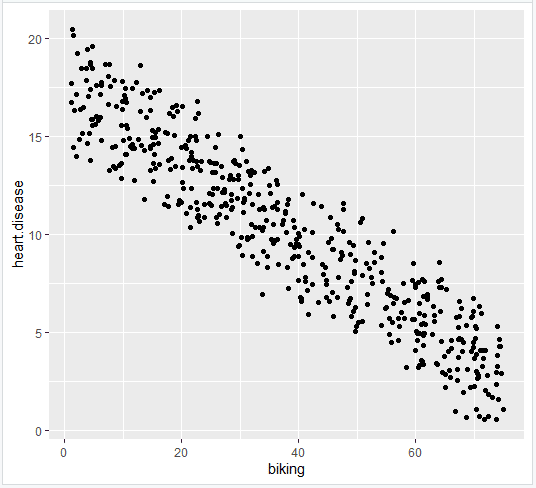
- Add the regression lines
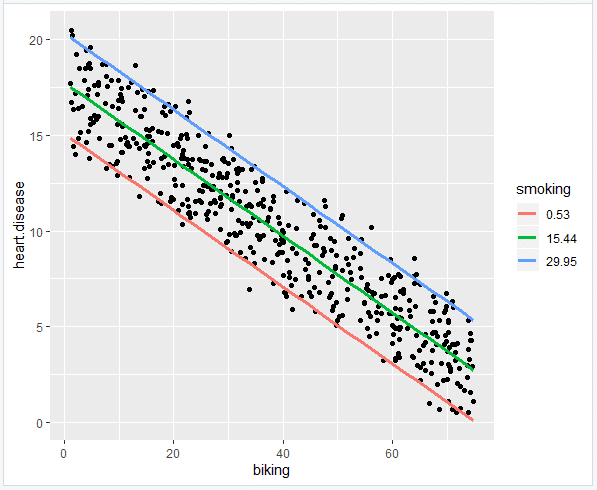
Because this graph has two regression coefficients, the stat_regline_equation() function won’t work here. But if we want to add our regression model to the graph, we can do so like this:
This is the finished graph that you can include in your papers!
In addition to the graph, include a brief statement explaining the results of the regression model.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Chi square test of independence
- Statistical power
- Descriptive statistics
- Degrees of freedom
- Pearson correlation
- Null hypothesis
Methodology
- Double-blind study
- Case-control study
- Research ethics
- Data collection
- Hypothesis testing
- Structured interviews
Research bias
- Hawthorne effect
- Unconscious bias
- Recall bias
- Halo effect
- Self-serving bias
- Information bias
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2024, May 09). Linear Regression in R | A Step-by-Step Guide & Examples. Scribbr. Retrieved June 18, 2024, from https://www.scribbr.com/statistics/linear-regression-in-r/
Is this article helpful?
Rebecca Bevans
Other students also liked, simple linear regression | an easy introduction & examples, multiple linear regression | a quick guide (examples), choosing the right statistical test | types & examples, what is your plagiarism score.
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
linearHypothesis function in R and interaction terms
I'm running the model:
model <- lm(y~ index1*gender +education, data=data)
and trying to test the null that the effect of index1 on y is 0 when gender=1 and am wondering if the following is the correct way to think about setting up this linear combination:
linearHypothesis(model, c('index1 + index1*gender = 0'))
- hypothesis-testing
- interaction
- 1 $\begingroup$ An asterisk can be used to indicate both the main effects and the corresponding interaction term in an R formula , but it can't be used for car 's linearHypothesis . Use a colon instead: "index1 + index1:gender = 0" . $\endgroup$ – Daeyoung Commented Mar 14, 2022 at 19:28
- $\begingroup$ Thanks @DaeyoungLim. Does this setup depend on whether the model has other controls, interactions, etc.? For example, the full model is: model <- lm(y~ index1*gender +education + index2*gender, data=data) $\endgroup$ – ZR8 Commented Mar 15, 2022 at 8:46
- $\begingroup$ That won’t matter. Interactions should be specified with colons $\endgroup$ – Daeyoung Commented Mar 15, 2022 at 12:05
Know someone who can answer? Share a link to this question via email , Twitter , or Facebook .
Your answer, sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Browse other questions tagged hypothesis-testing interaction or ask your own question .
- Featured on Meta
- Upcoming sign-up experiments related to tags
Hot Network Questions
- If "Good luck finding a new job" is sarcastic, how do change the sentence to make it sound well-intentioned?
- Going around in circles
- My supervisor is promoting my work (that I think has flaws) everywhere - what to do?
- What is the difference between "боля" and "болея"?
- Do rich parents pay less in child support if they didn't provide a rich lifestyle for their family pre-divorce?
- Does the recommendation to use password managers also apply to corporate environments?
- Movie with a gate guarded by two statues
- Best practices for relicensing what was once a derivative work
- LTCGY - Let the corners guide you
- Is it grammatically correct to say 'I suspect this clause to be a bit sloppy English'?
- Why are amber bottles used to store Water for HPLC?
- Is intrinsic spin a quantum or/and a relativistic phenomenon?
- Check if license plate number is formatted correctly
- Will it break Counterspell if the trigger becomes "perceive" instead of "see"?
- Short story crashing landing on a planet and taking shelter in a building that had automated defenses
- Is a judge's completely arbitrary determination of credibilty subject to appeal?
- How to make a low-poly version of a ramen bowl?
- Approximation algorithm for binary (linear) programs
- How did the `long` and `short` integer types originate?
- The term 'sfp' is not recognized
- Is there a maximum amount of time I should spend on an exercise bike?
- Advice for beginning cyclist
- Why can real number operations be applied to complex numbers?
- `ls` command stuck when run as root
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
3.6 - the general linear test.
This is just a general representation of an F -test based on a full and a reduced model. We will use this frequently when we look at more complex models.
Let's illustrate the general linear test here for the single factor experiment:
First we write the full model, \(Y_{ij} = \mu + \tau_i + \epsilon_{ij}\) and then the reduced model, \(Y_{ij} = \mu + \epsilon_{ij}\) where you don't have a \(\tau_i\) term, you just have an overall mean, \(\mu\). This is a pretty degenerate model that just says all the observations are just coming from one group. But the reduced model is equivalent to what we are hypothesizing when we say the \(\mu_i\) would all be equal, i.e.:
\(H_0 \colon \mu_1 = \mu_2 = \dots = \mu_a\)
This is equivalent to our null hypothesis where the \(\tau_i\)'s are all equal to 0.
The reduced model is just another way of stating our hypothesis. But in more complex situations this is not the only reduced model that we can write, there are others we could look at.
The general linear test is stated as an F ratio:
\(F=\dfrac{(SSE(R)-SSE(F))/(dfR-dfF)}{SSE(F)/dfF}\)
This is a very general test. You can apply any full and reduced model and test whether or not the difference between the full and the reduced model is significant just by looking at the difference in the SSE appropriately. This has an F distribution with ( df R - df F), df F degrees of freedom, which correspond to the numerator and the denominator degrees of freedom of this F ratio.
Let's take a look at this general linear test using Minitab...
Example 3.5: Cotton Weight Section

Remember this experiment had treatment levels 15, 20, 25, 30, 35 % cotton weight and the observations were the tensile strength of the material.
The full model allows a different mean for each level of cotton weight %.
We can demonstrate the General Linear Test by viewing the ANOVA table from Minitab:
STAT > ANOVA > Balanced ANOVA
The \(SSE(R) = 636.96\) with a \(dfR = 24\), and \(SSE(F) = 161.20\) with \(dfF = 20\). Therefore:
\(F^\ast =\dfrac{(636.96-161.20)/(24-20)}{161.20/20}\)
This demonstrates the equivalence of this test to the F -test. We now use the General Linear Test (GLT) to test for Lack of Fit when fitting a series of polynomial regression models to determine the appropriate degree of polynomial.
We can demonstrate the General Linear Test by comparing the quadratic polynomial model (Reduced model), with the full ANOVA model (Full model). Let \(Y_{ij} = \mu + \beta_{1}x_{ij} + \beta_{2}x_{ij}^{2} + \epsilon_{ij}\) be the reduced model, where \(x_{ij}\) is the cotton weight percent. Let \(Y_{ij} = \mu + \tau_i + \epsilon_{ij}\) be the full model.
The General Linear Test - Cotton Weight Example (no sound)
The video above shows the SSE ( R ) = 260.126 with dfR = 22 for the quadratic regression model. The ANOVA shows the full model with SSE ( F ) = 161.20 with dfF = 20.
Therefore the GLT is:
\(\begin{eqnarray} F^\ast &=&\dfrac{(SSE(R)-SSE(F))/(dfR-dfF)}{SSE(F)/dfF} \nonumber\\ &=&\dfrac{(260.126-161.200)/(22-20)}{161.20/20}\nonumber\\ &=&\dfrac{98.926/2}{8.06}\nonumber\\ &=&\dfrac{49.46}{8.06}\nonumber\\&=&6.14 \nonumber \end{eqnarray}\)
We reject \(H_0\colon \) Quadratic Model and claim there is Lack of Fit if \(F^{*} > F_{1}-\alpha (2, 20) = 3.49\).
Therefore, since 6.14 is > 3.49 we reject the null hypothesis of no Lack of Fit from the quadratic equation and fit a cubic polynomial. From the viewlet above we noticed that the cubic term in the equation was indeed significant with p -value = 0.015.
We can apply the General Linear Test again, now testing whether the cubic equation is adequate. The reduced model is:
\(Y_{ij} = \mu + \beta_{1}x_{ij} + \beta_{2}x_{ij}^{2} + \beta_{3}x_{ij}^{3} + \epsilon_{ij}\)
and the full model is the same as before, the full ANOVA model:
\(Y_ij = \mu + \tau_i + \epsilon_{ij}\)
The General Linear Test is now a test for Lack of Fit from the cubic model:
\begin{aligned} F^{*} &=\frac{(\operatorname{SSE}(R)-\operatorname{SSE}(F)) /(d f R-d f F)}{\operatorname{SSE}(F) / d f F} \\ &=\frac{(195.146-161.200) /(21-20)}{161.20 / 20} \\ &=\frac{33.95 / 1}{8.06} \\ &=4.21 \end{aligned}
We reject if \(F^{*} > F_{0.95} (1, 20) = 4.35\).
Therefore we do not reject \(H_A \colon\) Lack of Fit and conclude the data are consistent with the cubic regression model, and higher order terms are not necessary.

IMAGES
VIDEO
COMMENTS
F test statistic: 14.035; p-value: .003553; This particular hypothesis test uses the following null and alternative hypotheses: H 0: Both regression coefficients are equal to zero. H A: At least one regression coefficient is not equal to zero. Since the p-value of the test (.003553) is less than .05, we reject the null hypothesis.
A hypothesis test is a formal statistical test we use to reject or fail to reject some statistical hypothesis. This tutorial explains how to perform the following hypothesis tests in R: One sample t-test. Two sample t-test. Paired samples t-test. We can use the t.test () function in R to perform each type of test:
rhs. right-hand-side vector for hypothesis, with as many entries as rows in the hypothesis matrix; can be omitted, in which case it defaults to a vector of zeroes. For a multivariate linear model, rhs is a matrix, defaulting to 0. This argument isn't available for F-tests for linear mixed models. singular.ok.
Linear Hypothesis Tests Most regression output will include the results of frequentist hypothesis tests comparing each coefficient to 0. However, in many cases, you may be interested in whether a linear sum of the coefficients is 0. ... Linear hypothesis test in R can be performed for most regression models using the linearHypothesis() function ...
This tutorial covers basic hypothesis testing in R. Normality tests. Shapiro-Wilk normality test. Kolmogorov-Smirnov test. Comparing central tendencies: Tests with continuous / discrete data. One-sample t-test : Normally-distributed sample vs. expected mean. Two-sample t-test: Two normally-distributed samples.
6.2.2.1 Known Standard Deviation. It is simple to calculate a hypothesis test in R (in fact, we already implicitly did this in the previous section). When we know the population standard deviation, we use a hypothesis test based on the standard normal, known as a \(z\)-test.Here, let's assume \(\sigma_X = 2\) (because that is the standard deviation of the distribution we simulated from above ...
Test the general linear hypothesis C β ^ = d for the regression model reg. The test statistic is obtained from the formula: f = ( C β ^ − d) ′ ( C ( X ′ X) − 1 C ′) ( C β ^ − d) / r S S E / ( n − p) where. r is the number of contrasts contained in C, and. n-p is the model degrees of freedom. Under the null hypothesis, f will ...
Test the general linear hypothesis C \hat{\beta} = d C β^ =d for the regression model reg . The test statistic is obtained from the formula: f = \frac{(C \hat{\beta} - d)' ( C (X'X)^{-1} C' ) (C \hat{\beta} - d) / r }{. SSE / (n-p) } f = SSE/(n−p)(Cβ^−d) where. n-p is the model degrees of freedom. Under the null hypothesis, f will follow ...
hypothesis.matrix. matrix (or vector) giving linear combinations of coefficients by rows, or a character vector giving the hypothesis in symbolic form (see Details ). rhs. right-hand-side vector for hypothesis, with as many entries as rows in the hypothesis matrix; can be omitted, in which case it defaults to a vector of zeroes. test.
Using a binomial test, the p -value is < 0.0001. (Actually, R reports it as < 2.2e-16, which is shorthand for the number in scientific notation, 2.2 x 10 -16, which is 0.00000000000000022, with 15 zeros after the decimal point.) Assuming an alpha of 0.05, since the p -value is less than alpha, we reject the null hypothesis.
Hypothesis Testing for Two Samples: Two-Sample t-Test. ... Be mindful of linear regressions. They're not always the indicated statistical analysis. May 28. 4. Sheref Nasereldin, Ph.D. in ...
linearHypothesis() is a function in R that tests the general linear hypothesis for a model object for which a formula method exists, using a specified test statistic. It allows the user to define a broader set of null hypotheses than just assuming individual coefficients equal to zero. The linearHypothesis() function can be especially useful ...
The function lht also dispatches to linear.hypothesis. The hypothesis matrix can be supplied as a numeric matrix (or vector), the rows of which specify linear combinations of the model coefficients, which are tested equal to the corresponding entries in the righ-hand-side vector, which defaults to a vector of zeroes.
In the final part of the output we have the F-test and the R 2 values which assess the performance of the model as a whole. Residual standard error: 4.354 on 97 degrees of freedom Multiple R-squared: 0.8161, Adjusted R-squared: 0.8123 F-statistic: 215.2 on 2 and 97 DF, p-value: < 2.2e-16
An alternative linear hypothesis testing would be to test whether β1 or β2 are nonzero, so we jointly test the hypothesis β1=0 and β2 = 0 rather than testing each one at a time. Here the null is rejected when one is rejected. Rejection here means that at least one of your hypotheses can be rejected. In other words provide both linear ...
A general linear hypothesis refers to null hypotheses of the form H_0: K \theta = m for some parametric model model with parameter estimates coef ... an additional element focus is available storing the names of the factors under test. References. Frank Bretz, Torsten Hothorn and Peter Westfall (2010), Multiple Comparisons Using R, CRC Press ...
A linear hypothesis for a multivariate linear model (i.e., an object of class "mlm") can optionally include an intra-subject transformation matrix for a repeated-measures design. If the intra-subject transformation is absent (the default), the multivariate test concerns all of the corresponding coefficients for the response variables.
Although RESET test is widely used to test the linear hypothesis of a model, Dominguez and Lobato (2019) proposed a novel approach that generalizes well known specification tests such as Ramsey's. This test relies on wild-bootstrap; this package implements this approach to be usable with any function that fits linear models and is compatible ...
This video demonstrates how to test multiple linear hypotheses in R, using the linearHypothesis() command from the car library. As the car library does not ...
A linear hypothesis for a multivariate linear model (i.e., an object of class "mlm") can optionally include an intra-subject transformation matrix for a repeated-measures design. If the intra-subject transformation is absent (the default), the multivariate test concerns all of the corresponding coefficients for the response variables.
Table of contents. Getting started in R. Step 1: Load the data into R. Step 2: Make sure your data meet the assumptions. Step 3: Perform the linear regression analysis. Step 4: Check for homoscedasticity. Step 5: Visualize the results with a graph. Step 6: Report your results. Other interesting articles.
1. 1. An asterisk can be used to indicate both the main effects and the corresponding interaction term in an R formula, but it can't be used for car 's linearHypothesis. Use a colon instead: "index1 + index1:gender = 0". - Daeyoung.
The general linear test is stated as an F ratio: F = ( S S E ( R) − S S E ( F)) / ( d f R − d f F) S S E ( F) / d f F. This is a very general test. You can apply any full and reduced model and test whether or not the difference between the full and the reduced model is significant just by looking at the difference in the SSE appropriately.