simple harmonic motion powerpoint presentation

• My presentations

Auth with social network:

Download presentation

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

Presentation is loading. Please wait.

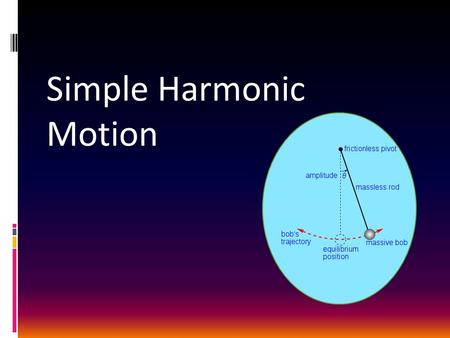
Simple Harmonic Motion

Published by Anis Reynolds Modified over 6 years ago

Similar presentations

Presentation on theme: "Simple Harmonic Motion"— Presentation transcript:

Vibrations and Waves Honors Physics.

Vibrations and Waves. SoundSection 1 What do you think? What is sound? What do all of the sounds that you hear have in common? How do they differ? Can.

Introduction to Oscillations and Simple Harmonic Motion

Chapter 14 Oscillations Chapter Opener. Caption: An object attached to a coil spring can exhibit oscillatory motion. Many kinds of oscillatory motion are.

Simple Harmonic Motion AP Physics 1. Simple Harmonic Motion Back and forth motion that is caused by a force that is directly proportional to the displacement.

Harmonic Motion AP Physics C.

AP Physics B Summer Course 年 AP 物理 B 暑假班 M Sittig Ch 17: Simple Harmonic Motion.

Elastic Potential Energy & Springs AP Physics C. Simple Harmonic Motion Back and forth motion that is caused by a force that is directly proportional.

Vibrations and Waves AP Physics Lecture Notes m Vibrations and Waves.

Chapter 11 - Simple Harmonic Motion

Vibrations and Waves Hooke’s Law Elastic Potential Energy Comparing SHM with Uniform Circular Motion Position, Velocity and Acceleration.

Simple Harmonic Motion Level 1 Physics. Simple Harmonic Motion When a force causes back and forth motion that is directly proportional to the displacement,

Springs We are used to dealing with constant forces. Springs are more complicated - not only does the magnitude of the spring force vary, the direction.

Vibrations and Waves m Physics 2053 Lecture Notes Vibrations and Waves.

About project

© 2024 SlidePlayer.com Inc. All rights reserved.

Chapter 14 - Simple Harmonic Motion

Apr 22, 2012

570 likes | 1.9k Views

Chapter 14 - Simple Harmonic Motion. A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University. © 2007. Photo by Mark Tippens.

Share Presentation

• acceleration reference circle
• conservation
• f simple harmonic motion
• f m summary simple
• whose constant
• torsion constant

Presentation Transcript

Chapter 14 - Simple Harmonic Motion A PowerPoint Presentation by Paul E. Tippens, Professor of Physics Southern Polytechnic State University © 2007

Photo by Mark Tippens A TRAMPOLINE exerts a restoring force on the jumper that is directly proportional to the average force required to displace the mat. Such restoring forces provide the driving forces necessary for objects that oscillate with simple harmonic motion.

Objectives: After finishing this unit, you should be able to: • Write and apply Hooke’s Law for objects moving with simple harmonic motion. • Write and apply formulas for finding the frequency f,period T,velocity v, or accelerationa in terms of displacementxor time t. • Describe the motion of pendulums and calculate the length required to produce a given frequency.

AmplitudeA Periodic Motion Simple periodic motion is that motion in which a body moves back and forth over a fixed path, returning to each position and velocity after a definite interval of time. Period, T, is the time for one complete oscillation. (seconds,s) Frequency, f, is the number of complete oscillations per second. Hertz (s-1)

x F Example 1:The suspended mass makes 30 complete oscillations in 15 s. What is the period and frequency of the motion? Period: T = 0.500 s Frequency: f = 2.00 Hz

x F Simple Harmonic Motion, SHM Simple harmonic motionis periodic motion in the absence of friction and produced by a restoring force that is directly proportional to the displacement and oppositely directed. A restoring force, F, actsin the direction opposite the displacement of the oscillating body. F = -kx

x F m DF Dx k = Hooke’s Law When a spring is stretched, there is a restoring force that is proportional to the displacement. F = -kx The spring constant k is a property of the spring given by:

x F m F (x) = kx F x1 x2 Work Done in Stretching a Spring Work done ONthe spring is positive; work BY spring is negative. From Hooke’s law the force F is: To stretch spring from x1 to x2 , work is: (Review module on work)

20 cm F m DF Dx 39.2 N 0.2 m k = = Example 2:A 4-kg mass suspended from a spring produces a displacement of 20 cm. What is the spring constant? The stretching force is the weight (W = mg) of the 4-kg mass: F = (4 kg)(9.8 m/s2) = 39.2 N Now, from Hooke’s law, the force constant k of the spring is: k = 196 N/m

8 cm F 0 m Example 2(cont.:The mass m is now stretched a distance of 8 cm and held. What is the potential energy? (k = 196 N/m) The potential energy is equal to the work done in stretching the spring: U = 0.627 J

x m x = -A x = 0 x = +A Displacement in SHM • Displacement is positive when the position is to the right of the equilibrium position (x = 0) and negative when located to the left. • The maximum displacement is called the amplitude A.

v (-) v (+) m x = -A x = 0 x = +A Velocity in SHM • Velocity is positive when moving to the right and negative when moving to the left. • It is zero at the end points and a maximum at the midpoint in either direction (+ or -).

+a -a -x +x m x = -A x = 0 x = +A Acceleration in SHM • Acceleration is in the direction of the restoring force. (a is positive when x is negative, and negative when x is positive.) • Acceleration is a maximum at the end points and it is zero at the center of oscillation.

a v x m x = -A x = 0 x = +A Acceleration vs. Displacement Given the spring constant, the displacement, and the mass, the acceleration can be found from: or Note: Acceleration is always opposite to displacement.

a +x m Example 3:A 2-kg mass hangs at the end of a spring whose constant is k = 400 N/m. The mass is displaced a distance of 12 cm and released. What is the acceleration at the instant the displacement is x = +7 cm? a = -14.0 m/s2 Note: When the displacement is +7 cm (downward), the acceleration is -14.0 m/s2 (upward) independent of motion direction.

+x m Example 4:What is the maximum acceleration for the 2-kg mass in the previous problem? (A = 12 cm, k = 400 N/m) The maximum acceleration occurs when the restoring force is a maximum; i.e., when the stretch or compression of the spring is largest. F = ma = -kx xmax =  A Maximum Acceleration: amax = ± 24.0 m/s2

a v x m x = -A x = 0 x = +A Conservation of Energy The total mechanical energy(U + K) of a vibrating system is constant; i.e., it is the same at any point in the oscillating path. For any two points A and B, we may write: ½mvA2 + ½kxA2 = ½mvB2 + ½kxB2

m a v x x = -A x = 0 x = +A Energy of a Vibrating System: A B • At points A and B, the velocity is zero and the acceleration is a maximum. The total energy is: U + K = ½kA2x =  A and v = 0. • At any other point: U + K = ½mv2 + ½kx2

m a v x x = -A x = 0 x = +A vmaxwhen x = 0: Velocity as Function of Position.

+x m Example 5:A 2-kg mass hangs at the end of a spring whose constant is k = 800 N/m. The mass is displaced a distance of 10 cm and released. What is the velocity at the instant the displacement is x = +6 cm? ½mv2 + ½kx 2 = ½kA2 v = ±1.60 m/s

0 +x m Example 5 (Cont.):What is the maximum velocity for the previous problem? (A = 10 cm, k = 800 N/m, m = 2 kg.) The velocity is maximum when x = 0: ½mv2 + ½kx 2 = ½kA2 v = ± 2.00 m/s

w = 2f The Reference Circle The reference circle compares the circular motion of an object with its horizontal projection. x = Horizontal displacement. A = Amplitude (xmax). q = Reference angle.

Velocity in SHM The velocity (v) of an oscillating body at any instant is the horizontal component of its tangential velocity (vT). vT = wR = wA; w = 2f v = -vTsin ;  = wt v = -wA sin w t v = -2f A sin 2ft

Acceleration Reference Circle The acceleration(a) of an oscillating body at any instant is the horizontal component of its centripetal acceleration (ac). a = -accos q = -ac cos(wt) R = A a = -w2A cos(wt)

The Period and Frequency as a Function of a and x. For any body undergoing simple harmonic motion: Since a = -4p2f2x and T = 1/f The frequency and the period can be found if the displacement and acceleration are known. Note that the signs of aand x will always be opposite.

Period and Frequency as a Function of Mass and Spring Constant. For a vibrating body with an elastic restoring force: Recall that F = ma = -kx: The frequencyfand the periodTcan be found if the spring constant k and mass m of the vibrating body are known. Use consistent SI units.

m a v x x = 0 x = -0.2 m x = +0.2 m Example 6:The frictionless system shown below has a 2-kg mass attached to a spring (k = 400 N/m). The mass is displaced a distance of 20 cm to the right and released.What is the frequency of the motion? f = 2.25 Hz

m a v x x = 0 x = -0.2 m x = +0.2 m Example 6 (Cont.):Suppose the 2-kg mass of the previous problem is displaced 20 cm and released (k = 400 N/m). What is the maximum acceleration? (f = 2.25 Hz) Acceleration is a maximum when x =  A a =  40 m/s2

m a v x x = 0 x = -0.2 m x = +0.2 m Example 6:The 2-kg mass of the previous example is displaced initially at x = 20 cm and released. What is the velocity 2.69 s after release? (Recall that f = 2.25 Hz.) v = -2f A sin 2ft (Note: q in rads) The minus sign means it is moving to the left. v = -0.916 m/s

-0.12 m m a v x x = 0 x = -0.2 m x = +0.2 m Example 7:At what time will the 2-kg mass be located 12 cm to the left of x = 0? (A = 20 cm, f = 2.25 Hz) t = 0.157 s

L mg The Simple Pendulum The period of a simple pendulum is given by: For small angles q.

L L = 0.993 m Example 8. What must be the length of a simple pendulum for a clock which has a period of two seconds (tick-tock)?

The Torsion Pendulum The period T of a torsion pendulum is given by: Where k’ is a torsion constant that depends on the material from which the rod is made; I is the rotational inertia of the vibrating system.

Example 9:A 160 g solid disk is attached to the end of a wire, then twisted at 0.8 rad and released. The torsion constant k’ is 0.025 N m/rad. Find the period. (Neglect the torsion in the wire) For Disk: I = ½mR2 I = ½(0.16 kg)(0.12 m)2 =0.00115 kg m2 T = 1.35 s Note: Period is independent of angular displacement.

x F m Summary Simple harmonic motion (SHM) is that motion in which a body moves back and forth over a fixed path, returning to each position and velocity after a definite interval of time. The frequency (rev/s) is the reciprocal of the period (time for one revolution).

x F m Summary (Cont.) Hooke’s Law: In a spring, there is a restoringforce that is proportional to the displacement. The spring constant k is defined by:

m a v x x = -A x = 0 x = +A Summary (SHM) Conservation of Energy: ½mvA2 + ½kxA2 = ½mvB2 + ½kxB2

Summary (SHM)

m a v x x = -A x = 0 x = +A Summary: Period and Frequency for Vibrating Spring.

L Summary: Simple Pendulum and Torsion Pendulum

CONCLUSION: Chapter 14Simple Harmonic Motion

• More by User

Simple Harmonic Motion

Simple Harmonic Motion. Simple harmonic motion: Motion that follows a repetitive pattern, caused by a restoring force that is proportional to displacement from the equilibrium position. In the case of this simple pendulum, what is the restoring force?. Simple Harmonic Oscillator: . F = - kx.

562 views • 8 slides

Simple Harmonic Motion. Spring Constant, K. The constant k is called the spring constant. SI unit of k = N/m. HOOKE'S LAW. The restoring force of an ideal spring is given by,.

312 views • 12 slides

Simple Harmonic Motion. Spring motion. Let’s assume that a mass is attached to a spring, pulled back, and allowed to move on a frictionless surface…. k. m. k. m. k. m. Simple Harmonic Motion (SHM).

584 views • 12 slides

Simple Harmonic Motion. Syll. State. 4.1.1-4.2.3 SS/Note template due next Monday (get note template from the website). Oscillations—what are they?. Repetitive, cyclical motion in which a mass (particle) moves back and forth around a single fixed point with a regular frequency

493 views • 13 slides

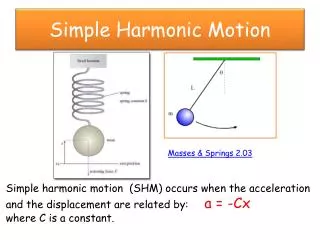
Simple Harmonic Motion. Masses & Springs 2.03. Simple harmonic motion (SHM) occurs when the acceleration and the displacement are related by: a = -Cx where C is a constant. Mass/Spring System. F = -kx ( Hooke’s Law) But F = ma so a = (-k/m)x SHM. The Displacement for SHM.

2.24k views • 8 slides

Simple Harmonic Motion. Pendulums & Longitudinal Waves. Simple Harmonic Motion…. …is a form of periodic motion (repeated motion). …is repeated motion over the same path. …requires a restoring force that is constantly pushing the mass to equilibrium position.

544 views • 9 slides

Simple Harmonic Motion. AP Physics B. Simple Harmonic Motion. Back and forth motion that is caused by a force that is directly proportional to the displacement. The displacement centers around an equilibrium position. Springs – Hooke’s Law.

560 views • 19 slides

Simple harmonic motion

Simple harmonic motion. SIMPLE HARMONIC MOTION. This unit is made up of the following: Reference circle (page 92 – 94). Graphs, Phasors & Equations (page 94 – 101). SHM of a spring (page 102 – 103). SHM of a pendulum (page 104). Energy of SHM. Forced SHM & Resonance (page 105 – 106).

1.13k views • 57 slides

Chapter 13 Simple Harmonic Motion

Chapter 13 Simple Harmonic Motion In chapter 13 we will study a special type of motion known as: simple harmonic motion (SHM). It is defined as the motion in which the position coordinate x of an object that moves along the x-axis varies with time t as:

754 views • 31 slides

Simple Harmonic Motion. Pre-AP Physics Pearland High School Mr. Dunk. Simple Harmonic Motion. simple harmonic motion (SHM) – vibration about an equilibrium position in which a restoring force is proportional to the displacement from equilibrium

511 views • 17 slides

Simple Harmonic Motion. What is Simple Harmonic Motion?. Simple harmonic motion (SHM) a type of wavelike motion that describes the behavior of many physical phenomena: a pendulum a bob attached to a spring low amplitude waves in air (sound), water, the ground

520 views • 11 slides

Simple Harmonic Motion. Oscillations. Motion is repetitive ( Periodic ) and the oscillating body moves back and forth around an equilibrium position. Period : The time required for one full oscillation We will focus on constant periods…

597 views • 30 slides

Simple Harmonic Motion. The single most important concept in the study of waves and sound is that of simple harmonic motion (SHM).

281 views • 12 slides

Chapter 11 Simple Harmonic Motion

Chapter 11 Simple Harmonic Motion. Chapter 11. Hooke’s Law. One type of periodic motion is the motion of a mass attached to a spring. The direction of the force acting on the mass ( F elastic ) is always opposite the direction of the mass’s displacement from equilibrium ( x = 0).

324 views • 22 slides

Simple Harmonic Motion. …an introduction. Simple Harmonic Motion. A periodic (repeating) motion that is the result of a restoring force which is proportional to the object’s displacement from rest position . A restoring force always pushes/pulls toward the rest position (equilibrium).

229 views • 7 slides

Simple Harmonic Motion. Physics. Simple Harmonic Motion. Back and forth motion that is caused by a force that is directly proportional to the displacement. The displacement centers around an equilibrium position. Springs – Hooke’s Law.

551 views • 19 slides

Simple Harmonic Motion. AP Physics C Mrs. Coyle. Periodic Motion. A motion of an object that repeats with a constant period. http://www.sccs.swarthmore.edu/users/08/ajb/e71/lab1/. Simple Harmonic Motion. It is a periodic motion. AND

470 views • 24 slides

Simple Harmonic Motion. A pendulum swinging from side to side is an example of both periodic and simple harmonic motion. Periodic motion is when an object continually moves back and forth over a definite path in equal intervals of time. Simple harmonic motion (SHM) is when the

419 views • 18 slides

Chapter 12 Simple Harmonic Motion

Chapter 12 Simple Harmonic Motion. Photo by Mark Tippens.

172 views • 15 slides

Simple Harmonic Motion. Mass on a compressible spring. Vertical mass-on-spring. Treat the equilibrium length of the spring as if it is the unstretched length of the spring. Then, you can neglect the gravitational force on the object. x(t) for SHO. Frequency and Stiffness.

157 views • 11 slides

Simple Harmonic Motion. Chapter 10 Sections 10.1 – 10.6. Simple harmonic motion. Simple harmonic motion is a cyclic motion produced by a a) mass & spring b) pendulum. Simple harmonic motion animation. Amplitude. Amplitude. Displacement x. 0. time t. Vocabulary.

238 views • 10 slides

• Preferences

Simple Harmonic Motion - PowerPoint PPT Presentation

Simple Harmonic Motion

Simple harmonic motion periodic motion when a vibration or oscillation repeats itself over the same time period oscillating spring system equilibrium position- where ... – powerpoint ppt presentation.

• When a vibration or oscillation repeats itself over the same time period
• Equilibrium position- where spring exerts no force on the mass (m)
• Natural state
• Spring stretched
• Exerts a force to move it back to equilibrium
• Spring compressed
• Force exerted pushing it back to equilibrium
• Force exerted when away from equilibrium
• - pulls it back to equilibrium
• Directly proportional to the displacement (x)
• k spring constant
• Greater the value of k the more force is needed to stretch spring - stiffer
• F is not constant, depends on x
• Therefore acceleration is not constant, depends on x
• At what position(s) is the acceleration the greatest?
• Where is it the least?
• Where is velocity greatest? And least?
• Amplitude (A) point of greatest displacement
• Cycle complete oscillation
• Period (T) time for one complete oscillation
• Frequency (f) cycles per second
• When a family of four people (total mass 200kg) steps into their 1200kg car, the springs compress 3.0 cm. A) What is the cars spring constant? B) How far will the car lower if loaded with 100kg of luggage as well?
• A .10 kg object is suspended from a spring with a spring constant of 10 N/m. The object is pulled 15cm from its equilibrium position and released, what is its maximum acceleration and when does it experience this?
• Any vibrating system where the restoring force is directly proportional to the negative displacement
• Any object exhibiting this is called a simple harmonic oscillator (SHO)

PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.

You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.

About the Developers

PowerShow.com is brought to you by  CrystalGraphics , the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.