case study ch 3 class 10 maths

• CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 3 - Pair of Linear Equations in Two Variables (Published by CBSE)

Cbse's question bank on case study for class 10 maths chapter 3 is available here. these questions will be very helpful to prepare for the cbse class 10 maths exam 2022..

Case study questions are going to be new for CBSE Class 10 students. These are the competency-based questions that are completely new to class 10 students. To help students understand the format of the questions, CBSE has released a question bank on case study for class 10 Maths. Students must practice with these questions to get familiarised with the concepts and logic used in the case study and understand how to answers them correctly. You may check below the case study questions for CBSE Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables. You can also check the right answer at the end of each question.

Check Case Study Questions for Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables

CASE STUDY-1:

1. If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly?

2. How many questions did he guess?

3. If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?

4. If answer to all questions he attempted by guessing were wrong, then how many questions answered correctly to score 95 marks?

Let the no of questions whose answer is known to the student x and questions attempted by cheating be y

x – 1/4y =90

solving these two

x = 96 and y = 24

1. He answered 96 questions correctly.

2. He attempted 24 questions by guessing.

3. Marks = 80- ¼ 0f 40 =70

4. x – 1/4 of (120 – x) = 95

5x = 500, x = 100

CASE STUDY-2:

Amit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is 95 sq.m.

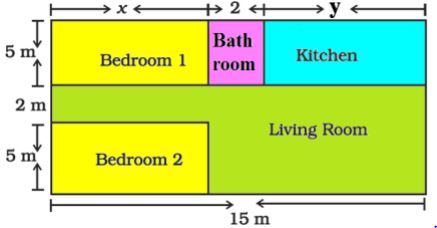
Based on the above information, answer the following questions:

1. Form the pair of linear equations in two variables from this situation.

2. Find the length of the outer boundary of the layout.

3. Find the area of each bedroom and kitchen in the layout.

4. Find the area of living room in the layout.

5. Find the cost of laying tiles in kitchen at the rate of Rs. 50 per sq.m.

1. Area of two bedrooms= 10x sq.m

Area of kitchen = 5y sq.m

10x + 5y = 95

Also, x + 2+ y = 15

2. Length of outer boundary = 12 + 15 + 12 + 15 = 54m

3. On solving two equation part(i)

x = 6m and y = 7m

area of bedroom = 5 x 6 = 30m

area of kitchen = 5 x 7 = 35m

4. Area of living room = (15 x 7) – 30 = 105 – 30 = 75 sq.m

5. Total cost of laying tiles in the kitchen = Rs50 x 35 = Rs1750

Case study-3 :

It is common that Governments revise travel fares from time to time based on various factors such as inflation ( a general increase in prices and fall in the purchasing value of money) on different types of vehicles like auto, Rickshaws, taxis, Radio cab etc. The auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations:

Related Stories

CBSE Class 10 Science Reflection and Refraction Competency-Based Questions With Answer Key 2024-25: Chapter 9 FREE PDF Download

CBSE Class 10 Science Heredity Competency-Based Questions With Answer Key 2024-25: Chapter 5 FREE PDF Download

NCERT Exemplar Class 10: Download All Chapters in PDF Here!

Situation 1: In city A, for a journey of 10 km, the charge paid is Rs 75 and for a journey of 15 km, the charge paid is Rs 110.

Situation 2: In a city B, for a journey of 8km, the charge paid is Rs91 and for a journey of 14km, the charge paid is Rs 145.

Refer situation 1

1. If the fixed charges of auto rickshaw be Rs x and the running charges be Rs y km/hr, the pair of linear equations representing the situation is

a) x + 10y =110, x + 15y = 75

b) x + 10y = 75, x + 15y = 110

c) 10x + y = 110, 15x + y = 75

d) 10x + y = 75, 15x + y = 110

Answer: b) x + 10y = 75, x + 15y = 110

2. A person travels a distance of 50km. The amount he has to pay is

Answer: c) Rs.355

Refer situation 2

3. What will a person have to pay for travelling a distance of 30km?

Answer: b) Rs.289

4. The graph of lines representing the conditions are: (situation 2)

Answer: (iii)

Also Check:

CBSE Case Study Questions for Class 10 Maths - All Chapters

Tips to Solve Case Study Based Questions Accurately

Get here latest School , CBSE and Govt Jobs notification and articles in English and Hindi for Sarkari Naukari , Sarkari Result and Exam Preparation . Download the Jagran Josh Sarkari Naukri App .

• OTET Result 2024
• RRB ALP Paper Analysis 2024
• RRB ALP Admit Card 2024
• SSC MTS Answer Key 2024
• SSC CGL Result 2024
• RRB ALP Exam Analysis 2024
• UP Police Result 2024
• CBSE Exam Date Sheet 2025
• CBSE 12th Date Sheet 2025
• CBSE 10th Date Sheet 2025 PDF
• Education News
• CBSE Study Material
• CBSE Class 10

Latest Education News

ICSE Class 10 Date Sheet 2025: ICSE Exam Date, Download Time Table

(Link Active) JKSSB Police Constable Admit Card 2024 Out at jkssb.nic.in: Here's Direct Hall Ticket Download Link for 4002 Vacancies

RSMSSB LDC Result 2024 Live Updates: Rajasthan Junior Assistant, Clerk Result Out at rsmssb.rajasthan.gov.in

(Link Active) RSMSSB LDC Result 2024 Out at rsmssb.rajasthan.gov.in: Download Clerk, Junior Assistant Result and cut off marks

ICSE Date Sheet 2025 Out: Download CISCE Class X Time Table PDF at cisce.org

ICSE, ISC Date Sheet 2025 Released: Download CISCE Class X, CLass XII Time Table PDF at cisce.org

ISC Date Sheet 2025 Out: Download CISCE Class XII Time Table PDF at cisce.org

RSMSSB LDC Cut Off 2024 Out: Gen, OBC, SC, ST Minimum Qualifying Marks Here

Picture Puzzle IQ Test: Only 2% With Most Attentive Eyes Can Spot the Mistake in 4 Seconds!

IPL Auction 2025: दूसरे दिन किस टीम ने किस खिलाड़ी पर उड़ाया कितना पैसा, टीम-वाइज पूरी लिस्ट यहां देखें

IPL 2025 RCB Players: RCB ने तैयार की धाकड़ टीम, अगले सीजन में दिखेंगे ये खिलाड़ी

(OUT) RSMSSB LDC Result @rsmssb.rajasthan.gov.in Live Update 2024: यहाँ से Download करें राजस्थान एलडीसी, जूनियर असिस्टेंट और फारेस्ट गार्ड रिजल्ट का परिणाम PDF

Rajasthan Pashu Parichar Admit Card 2024 जारी, ये रहा Direct Link

MI Team 2025 Players List, Price: Check Complete Mumbai Indians Squad and Overview

RCB Team 2025 Players List, Price: Check Complete Royal Challengers Bengaluru Squad and Overview

PBK Team 2025 Players List, Price: Check Punjab Kings Squad, Captain and Coach

SC Rules: Socialist and Secular in Preamble are Constitutionally Valid

DC Team 2025 Players List, Price: Check Complete Delhi Capitals Squad and Overview

RSMSSB Rajasthan LDC Cut Off 2024 OUT: GEN, OBC, SC और ST कैटेगरी के लिए देखें कट ऑफ

KKR Team 2025 Players List, Price: Check Complete Kolkata Knight Riders Squad and Overview

Class 10 Maths Case Study Questions Chapter 3 Pair of Linear Equations in Two Variables

• Post author: studyrate
• Post published:
• Post category: class 10th
• Post comments: 0 Comments

Case study Questions in the Class 10 Mathematics Chapter 3  are very important to solve for your exam. Class 10 Maths Chapter 3 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based   questions for Class 10 Maths Chapter 3  Pair of Linear Equations in Two Variables

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Pair of Linear Equations in Two Variables Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 10 Maths  Chapter 3 Pair of Linear Equations in Two Variables

Case Study/Passage-Based Questions

(i) 1 st  situation can be represented algebraically as

Answer: (d) 2x+3y=46

(ii) 2 nd  situation can be represented algebraically as

Answer: (c) 3x + 5y = 74

(iii), Fare from Ben~aluru to Malleswaram is

Answer: (b) Rs 8

(iv) Fare from Bengaluru to Yeswanthpur is

Answer: (a) Rs 10

(v) The system oflinear equations represented by both situations has

Answer: (c) unique solution

Case Study 2: The scissors which are so common in our daily life use, its blades represent the graph of linear equations.

Let the blades of a scissor are represented by the system of linear equations:

x + 3y = 6 and 2x – 3y = 12

(i) The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x – 3y = 12 of the scissor is (a) (2, 3) (b) (6, 0) (c) (3, 2) (d) (2, 6)

Answer: (b) (6, 0)

(ii) The points at which linear equations x + 3y = 6 and 2x – 3y = 12 intersect y – axis respectively are (a) (0, 2) and (0, 6) (b) (0, 2) and (6, 0) (c) (0, 2) and (0, –4) (d) (2, 0) and (0, –4)

Answer: (c) (0, 2) and (0, –4)

(iii) The number of solution of the system of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 is (a) 0 (b) 1 (c) 2 (d) infinitely many

Answer: (d) infinitely many

(iv) If (1, 2) is the solution of linear equations ax + y = 3 and 2x + by = 12, then values of a and b are respectively (a) 1, 5 (b) 2, 3 (c) –1, 5 (d) 3, 5

Answer: (a) 1, 5

(v) If a pair of linear equations in two variables is consistent, then the lines represented by two equations are (a) intersecting (b) parallel (c) always coincident (d) intersecting or coincident

Answer: (d) intersecting or coincident

Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 10 Maths Pair of Linear Equations in Two Variables Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

You Might Also Like

Cbse class 10 english term 2 mcq questions with answers pdf download, extra questions of class 10 social science history chapter 6 work, life and leisure pdf download, case study questions class 10 science chapter 5 periodic classification of elements, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Important Question
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• Question Bank
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• Toppers Notes
• Most Repeated Question
• Diagram Based Question
• Study Planner
• Competency Based Questions
• JEE Previous Year Paper
• JEE Mock Test
• JEE Crash Course
• JEE Sample Papers
• JEE Toppers Notes
• JEE Formula
• JEE Important Question
• JEE Mind Map
• JEE Integer-Numerical Type Question
• JEE Study Planner
• Important Info
• SRM-JEEE Previous Year Paper
• SRM-JEEE Mock Test
• VITEEE Previous Year Paper
• VITEEE Mock Test
• BITSAT Previous Year Paper
• BITSAT Mock Test
• Manipal Previous Year Paper
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• AP EAMCET Mock Test
• COMEDK Previous Year Paper
• COMEDK Mock Test
• GUJCET Previous Year Paper
• GUJCET Mock Test
• KCET Previous Year Paper
• KCET Mock Test
• KEAM Previous Year Paper
• KEAM Mock Test
• MHT CET Previous Year Paper
• MHT CET Mock Test
• TS EAMCET Previous Year Paper
• TS EAMCET Mock Test
• WBJEE Previous Year Paper
• WBJEE Mock Test
• AMU Previous Year Paper
• AMU Mock Test
• CUSAT Previous Year Paper
• CUSAT Mock Test
• AEEE Previous Year Paper
• AEEE Mock Test
• UPSEE Previous Year Paper
• UPSEE Mock Test
• CGPET Previous Year Paper
• BCECE Previous Year Paper
• JCECE Previous Year Paper
• LPU Mock Test
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• NEET Toppers Notes
• NEET Formula
• NEET Important Question
• NEET Assertion Reason Question
• NEET Study Planner
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• Verbal Ability & Reading Comprehension
• Logical Reasoning & Data Interpretation
• CAT Mock Test
• CAT Important Question
• CAT Vocabulary
• CAT English Grammar
• MBA General Knowledge
• CAT Mind Map
• CAT Study Planner
• CMAT Mock Test
• SRCC GBO Mock Test
• SRCC GBO PYQs
• XAT Mock Test
• SNAP Mock Test
• IIFT Mock Test
• MAT Mock Test
• CUET PG Mock Test
• CUET PG PYQs
• MAH CET Mock Test
• MAH CET PYQs
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

Case Study on Pair of Equations in Two Variables Class 10 Maths PDF

The passage-based questions are commonly known as case study questions. Students looking for Case Study on Pair of Equations in Two Variables Class 10 Maths can use this page to download the PDF file. 

The case study questions on Pair of Equations in Two Variables are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Pair of Equations in Two Variables case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.

Case Study on Pair of Equations in Two Variables Class 10 Maths with Solutions in PDF

Our experts have also kept in mind the challenges students may face while solving the case study on Pair of Equations in Two Variables, therefore, they prepared a set of solutions along with the case study questions on Pair of Equations in Two Variables.

The case study on Pair of Equations in Two Variables Class 10 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Pair of Equations in Two Variables case study questions are very easy to grasp from the PDF - download links are given on this page.

Why Solve Pair of Equations in Two Variables Case Study Questions on Class 10 Maths?

There are three major reasons why one should solve Pair of Equations in Two Variables case study questions on Class 10 Maths - all those major reasons are discussed below:

• To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 10 Maths students, therefore, it is important to solve Pair of Equations in Two Variables Case study questions as it will help better prepare for the Class 10 board exam preparation.
• Develop Problem-Solving Skills: Class 10 Maths Pair of Equations in Two Variables case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any profession rather than Class 10 board exam preparation.
• Understand Real-Life Applications: Several Pair of Equations in Two Variables Class 10 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Pair of Equations in Two Variables as well as real-life implications of those learnings too.

How to Answer Case Study Questions on Pair of Equations in Two Variables?

Students can choose their own way to answer Case Study on Pair of Equations in Two Variables Class 10 Maths, however, we believe following these three steps would help a lot in answering Class 10 Maths Pair of Equations in Two Variables Case Study questions.

• Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
• Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Pair of Equations in Two Variables questions quickly.
• Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Pair of Equations in Two Variables Class 10 Maths case study questions make sure you are approaching each question in a step-wise manner.

What to Know to Solve Case Study Questions on Class 10 Pair of Equations in Two Variables?

 A few essential things to know to solve Case Study Questions on Class 10 Pair of Equations in Two Variables are -

• Basic Formulas of Pair of Equations in Two Variables: One of the most important things to know to solve Case Study Questions on Class 10 Pair of Equations in Two Variables is to learn about the basic formulas or revise them before solving the case-based questions on Pair of Equations in Two Variables.
• To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 10 Maths Pair of Equations in Two Variables case study questions.
• Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.

Where to Find Case Study on Pair of Equations in Two Variables Class 10 Maths?

Use Selfstudys.com to find Case Study on Pair of Equations in Two Variables Class 10 Maths. For ease, here is a step-wise procedure to download the Pair of Equations in Two Variables Case Study for Class 10 Maths in PDF for free of cost.

Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Pair of Equations in Two Variables. To help others reach this page let them know these steps:

• Open Selfstudys.com on your computer/laptop or Smartphone 
• Once the website gets loaded, click on the navigation button

• Find CBSE from the given menu

• Click on Case Study

• Choose Class 10 
• Search Maths and then navigate to the Pair of Equations in Two Variables Class 10 Maths Case Study

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences

One Last Step...

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

Class 10 Maths Chapter 3 Case Based Questions - Pair of Linear Equations in Two Variables

Case study - 1.

Refer situation 1 : Q1: If the fixed charges of auto rickshaw be Rs x and the running charges be Rs y km/hr, the pair of linear equations representing the situation is (a) x + 10y =110, x + 15y = 75 (b) x + 10y = 75, x + 15y = 110 (c) 10x + y = 110, 15x + y = 75 (d) 10x + y = 75, 15x + y = 110 Ans: (b) Explanation:  The cost of the auto rickshaw ride consists of two components - a fixed charge (x) and a variable charge based on the distance of the journey (y per km). The total cost of the ride would therefore be the sum of these two components. In the first situation, the auto rickshaw ride in city A costs Rs 75 for a 10 km journey and Rs 110 for a 15 km journey. We can express these two situations as two linear equations: For the 10 km journey: x + 10y = 75 (equation 1) For the 15 km journey: x + 15y = 110 (equation 2) Where x is the fixed charge and y is the cost per km. Therefore, the pair of linear equations representing the situation is x + 10y = 75, x + 15y = 110 (option b).   Q2: A person travels a distance of 50km. The amount he has to pay is (a) Rs.155 (b) Rs.255 (c) Rs.355 (d) Rs.455 Ans:  (c) Explanation:  To solve this case-based problem, we first need to understand the relationship between distance traveled and the charge paid. This can be represented as a linear equation in the form of y = mx + c, where y is the charge paid, m is the rate charged per km, x is the distance traveled, and c is the fixed charge. From Situation 1, we have two equations based on the given data: 1) 75 = 10m + c 2) 110 = 15m + c Subtracting equation 1 from equation 2, we get: 35 = 5m So, m = 35/5 = 7. This means the rate charged per km in city A is Rs. 7. Substituting m = 7 in equation 1, we get: 75 = 10*7 + c So, c = 75 - 70 = 5. This means the fixed charge in city A is Rs. 5. So, the total charge for traveling a distance of x km in city A is given by the equation: Charge = 7x + 5 Now, let's calculate the charge for traveling a distance of 50km in city A: Charge = 7*50 + 5 = Rs. 355 Therefore, the answer is (c) Rs. 355.   Refer situation 2: Q3: What will a person have to pay for travelling a distance of 30km? (a) Rs.185 (b) Rs.289 (c) Rs.275 (d) Rs.305 Ans:  (b) Explanation:  To solve this problem, we first need to find the rate of the fare per kilometer and the fixed charge in city B. We can solve this problem by making two equations from the given situations and then solve them simultaneously. Let's take the fixed charge as F (in Rs.) and the rate per kilometer as R (in Rs. per km). From the given situation 2, we know that: For a journey of 8km, the charge paid is Rs 91. For a journey of 14km, the charge paid is Rs 145. So, we can formulate two equations: 1) F + 8R = 91 2) F + 14R = 145 Subtract equation 1 from equation 2 and we get 6R = 54, therefore R = 54/6 = 9 Rs per km. Substitute the value of R in equation 1, we get F = 91 - 8*9 = 91 - 72 = 19 Rs. So, the fixed charge is Rs 19 and the fare per kilometer is Rs 9 in city B. Now, to find out what a person will have to pay for traveling a distance of 30km, we add the fixed charge to the product of the fare per kilometer and the distance. Therefore, the fare for 30km = F + 30R = 19 + 30*9 = 19 + 270 = Rs 289. So, the correct answer is (b) Rs.289.  

Case Study - 2

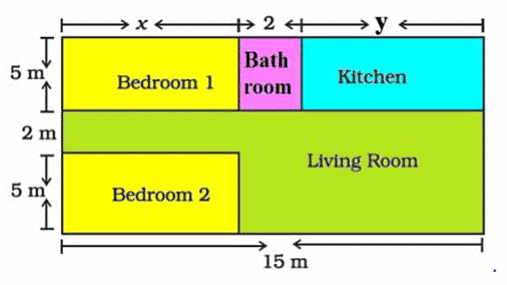
Based on the above information, answer the following questions: Q1: Form the pair of linear equations in two variables from this situation. Ans: Area of two bedrooms= 10x sq.m Area of kitchen = 5y sq.m 10x + 5y = 95 2x + y =19 Also, x + 2+ y = 15 x + y = 13 Q2: Find the length of the outer boundary of the layout. Ans:  Length of outer boundary = 12 + 15 + 12 + 15 = 54m   Q3: Find the area of each bedroom and kitchen in the layout. Ans:  On solving two equation part(i) x = 6m and y = 7m area of bedroom = 5 x 6 = 30m area of kitchen = 5 x 7 = 35m Q4: Find the area of living room in the layout. Ans:  Area of living room = (15 x 7) – 30 = 105 – 30 = 75 sq.m   Q5: Find the cost of laying tiles in kitchen at the rate of Rs. 50 per sq.m. Ans:  Total cost of laying tiles in the kitchen = Rs.50 x 35 = Rs1750.

Case Study - 3

A test consists of ‘True’ or ‘False’ questions. One mark is awarded for every correct answer while ¼ mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing. He answered 120 questions and got 90 marks.

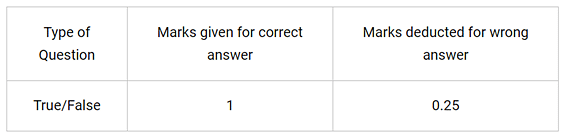
Q2: How many questions did he guess? Ans:  Let the no of questions whose answer is known to the student x and questions attempted by cheating be y x + y =120 x – 1/4y =90 solving these two x = 96 and y = 24 He attempted 24 questions by guessing.   Q3: If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got? Ans:  Let the no of questions whose answer is known to the student x and questions attempted by cheating be y x + y =120 x – 1/4y =90 solving these two x = 96 and y = 24 Marks = 80- ¼ 0f 40 =70

Q4: If answer to all questions he attempted by guessing were wrong, then how many questions answered correctly to score 95 marks? Ans:  Let the no of questions whose answer is known to the student x and questions attempted by cheating be y x + y =120 x – 1/4y =90 solving these two x = 96 and y = 24 x – 1/4 of (120 – x) = 95 5x = 500, x = 100

Top Courses for Class 10

Important questions, extra questions, shortcuts and tricks, past year papers, practice quizzes, mock tests for examination, study material, sample paper, objective type questions, previous year questions with solutions, video lectures, viva questions, semester notes.

Case Based Questions: Pair of Linear Equations in Two Variables Free PDF Download

Importance of case based questions: pair of linear equations in two variables, case based questions: pair of linear equations in two variables notes, case based questions: pair of linear equations in two variables class 10, study case based questions: pair of linear equations in two variables on the app, welcome back, create your account for free.

Forgot Password

Change country.

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

• Last modified on: 1 year ago
• Reading Time: 5 Minutes

Case Study Questions

Question 1:

The scissors which is so common in our daily life use, its blades represent the graph of linear equations.

Let the blades of a scissor are represented by the system of linear equations:

x + 3y = 6 and 2x – 3y = 12

(i) The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x – 3y = 12 of the scissor is (a) (2, 3) (b) (6, 0) (c) (3, 2) (d) (2, 6)

(ii) The points at which linear equations x + 3y = 6 and 2x – 3y = 12 intersect y – axis respectively are (a) (0, 2) and (0, 6) (b) (0, 2) and (6, 0) (c) (0, 2) and (0, –4) (d) (2, 0) and (0, –4)

(iii) The number of solution of the system of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 is (a) 0 (b) 1 (c) 2 (d) infinitely many

(iv) If (1, 2) is the solution of linear equations ax + y = 3 and 2x + by = 12, then values of a and b are respectively (a) 1, 5 (b) 2, 3 (c) –1, 5 (d) 3, 5

(v) If a pair of linear equations in two variables is consistent, then the lines represented by two equations are (a) intersecting (b) parallel (c) always coincident (d) intersecting or coincident

✨ Free Quizzes, Test Series and Learning Videos for CBSE Class 10 Maths

You may also like:

Chapter 1 Real Numbers Chapter 2 Polynomials Chapter 3 Pair of Linear Equations in Two Variables C hapter 4 Quadratic Equations Chapter 5 Arithmetic Progressions Chapter 6 Triangles Chapter 7 Coordinate Geometry Chapter 8 Introduction to Trigonometry Chapter 9 Some Applications of Trigonometry Chapter 10 Circles Chapter 11 Constructions Chapter 12 Areas Related to Circles Chapter 13 Surface Areas and Volumes Chapter 14 Statistics Chapter 15 Probability

Download Books – Exam Special

Sample Papers for CBSE 2025 Exams

• Sample Question Papers for CBSE Class 8 All Subjects (for 2025 Exams)
• Sample Question Papers for CBSE Class 9 All Subjects (for 2025 Exams)
• Sample Question Papers for CBSE Class 10 All Subjects (for 2025 Exams)
• Sample Question Papers for CBSE Class 12 All Subjects (for 2025 Exams)

CBSE Class 10 Most Downloaded Books

• CBSE Important Numerical Problems Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Most Repeated Questions for Class 10 Science Board Exams

CBSE Class 12 Most Downloaded Books

• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Class 12 Physics Chapterwise Important Questions

CBSE Class 8 Most Downloaded Books

• Worksheets for CBSE Class 8 Maths – Chapterwise

ICSE Class 10

• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)
• ICSE Reasoning Based Questions Class 10 Geography BOARD Exams
• ICSE Revision Notes for Class 10 Chemistry BOARD Exams
• ICSE Revision Notes for Class 10 Physics BOARD Exams

ICSE Class 9

• ICSE Important Figure Based Questions Class 9 Physics Exams
• ICSE Important Numerical Problems for Class 9 Physics Exams
• ICSE Reasoning Based Questions Class 9 Geography BOARD Exams (150 Qs)

CBSE Chapter-Wise Test Papers

• CBSE Class 9 Science Chapterwise Test Papers
• CBSE Class 10 Science Chapterwise Test Papers
• CBSE Class 10 Maths Chapterwise Test Papers
• CBSE Class 10 Social Science Chapterwise Test Papers
• CBSE Class 12 Physics Chapterwise Test Papers
• CBSE Class 12 Chemistry Chapterwise Test papers

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

• New QB365-SLMS
• 12th Standard Materials
• 11th Standard Materials
• 10th Standard Materials
• 9th Standard Materials
• 8th Standard Materials
• 7th Standard Materials
• 6th Standard Materials
• 12th Standard CBSE Materials
• 11th Standard CBSE Materials
• 10th Standard CBSE Materials
• 9th Standard CBSE Materials
• 8th Standard CBSE Materials
• 7th Standard CBSE Materials
• 6th Standard CBSE Materials
• Tamilnadu Stateboard
• Scholarship Exams
• Scholarships

CBSE 10th Standard Maths Subject Case Study Questions With Solution 2021 Part - II

By QB365 on 21 May, 2021

QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get  more marks in Exams

QB365 - Question Bank Software

10th Standard CBSE

Final Semester - June 2015

Case Study Questions

(ii) Proportional expense for each person is

(iii) The fixed (or constant) expense for the party is

(iv) If there would be 15 guests at the lunch party, then what amount Mr Jindal has to pay?

(v) The system of linear equations representing both the situations will have

(ii) Represent the situation faced by Suman, algebraically

(iii) The price of one Physics book is

(iv) The price of one Mathematics book is

(v) The system of linear equations represented by above situation, has

(ii) Represent algebraically the situation of day- II.

(iii) The linear equation represented by day-I, intersect the x axis at

(iv) The linear equation represented by day-II, intersect the y-axis at

(v) Linear equations represented by day-I and day -II situations, are

Amit is preparing for his upcoming semester exam. For this, he has to practice the chapter of Quadratic Equations. So he started with factorization method. Let two linear factors of  \(a x^{2}+b x+c \text { be }(p x+q) \text { and }(r x+s)\) \(\therefore a x^{2}+b x+c=(p x+q)(r x+s)=p r x^{2}+(p s+q r) x+q s .\) Now, factorize each of the following quadratic equations and find the roots. (i) 6x 2 + x - 2 = 0

(ii) 2x 2 -+ x - 300 = 0

(iii) x 2 -  8x + 16 = 0

(iv) 6x 2 -  13x + 5 = 0

(v) 100x 2 - 20x + 1 = 0

(ii) Difference of pairs of shoes in 17 th  row and 10 th row is

(iii) On next day, she arranges x pairs of shoes in 15 rows, then x =

(iv) Find the pairs of shoes in 30 th row.

(v) The total number of pairs of shoes in 5 th and 8 th row is

(ii) The number on first card is

(iii) What is the number on the 19 th card?

(iv) What is the number on the 23 rd card?

(v) The sum of numbers on the first 15 cards is 

A sequence is an ordered list of numbers. A sequence of numbers such that the difference between the consecutive terms is constant is said to be an arithmetic progression (A.P.). On the basis of above information, answer the following questions. (i) Which of the following sequence is an A.P.?

(ii) If x, y and z are in A.P., then

(iii) If a 1  a 2 , a 3  ..... , a n are in A.P., then which of the following is true?

(iv) If the n th term (n > 1) of an A.P. is smaller than the first term, then nature of its common difference (d) is

(v) Which of the following is incorrect about A.P.?

(ii) Find the radius of the core.

(iii) S 2 =

(iv) What is the diameter of roll when one tissue sheet is rolled over it?

(v) Find the thickness of each tissue sheet

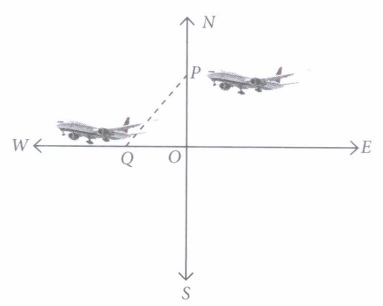
(ii) Distance travelled by aeroplane towards west after   \(1 \frac{1}{2}\)   hr is

(iii) In the given figure, \(\angle\) POQ is 

(iv) Distance between aeroplanes after  \(1 \frac{1}{2}\)   hr is

(v) Area of \(\Delta\) POQ is

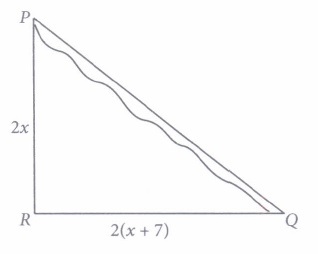
(ii) The value of x is

(iii) The value of PR is 

(iv) The value of RQ is 

(v) How much distance will be saved in reaching city Q after the construction of highway? 

(ii) Length of BC =

(iii) Length of AD =

(iv) Length of ED = 

(v) Length of AE = 

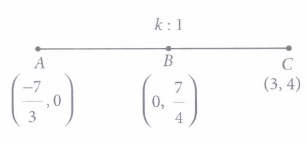
(ii) The value of x + y is 

(iii) Which of the following is true?

(iv) The ratio in which B divides AC is

(v) Which of the following equations is satisfied by the given points?

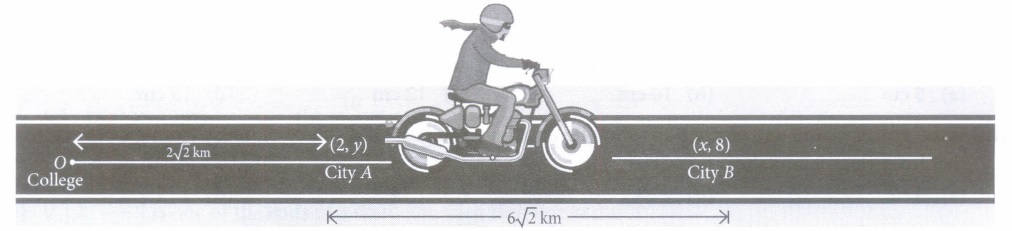
(ii) The value of x is equal to

(iii) If M is any point exactly in between city A and city B, then coordinates of M are

(iv) The ratio in which A divides the line segment joining the points O and M is

(v) If the person analyse the petrol at the point M(the mid point of AB), then what should be his decision?

(ii) The centre of circle is the

(iii) The radius of the circle is

(iv) The area of the circle is

(v) If  \(\left(1, \frac{\sqrt{7}}{3}\right)\)   is one of the ends of a diameter, then its other end is

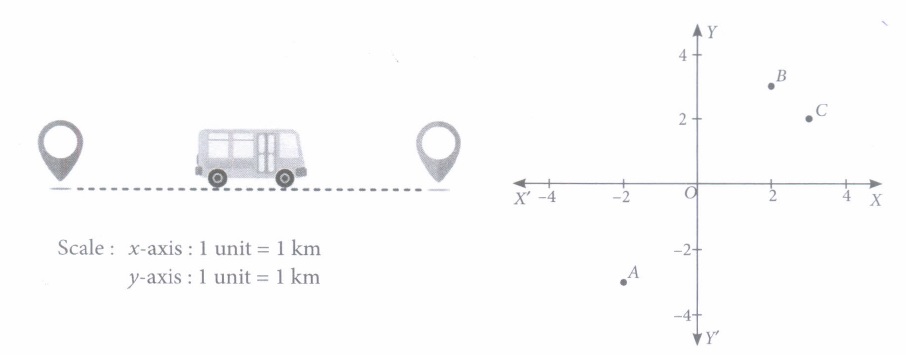
(ii) The distance between A and Cis

(iii) If it is assumed that both buses have same speed, then by which bus do you want to travel from A to B?

(iv) If the fare for first bus is Rs10/km, then what will be the fare for total journey by that bus?

(v) If the fare for second bus is Rs 15/km, then what will be the fare to reach to the destination by this bus?

*****************************************

Cbse 10th standard maths subject case study questions with solution 2021 part - ii answer keys.

(i) (a): 1 st situation can be represented as x + 7y = 650 ...(i) and 2 nd situation can be represented as x + 11y = 970 ...(ii) (ii) (b): Subtracting equations (i) from (ii), we get  \(4 y=320 \Rightarrow y=80\) \(\therefore\)  Proportional expense for each person is Rs 80. (iii) (c): Puttingy = 80 in equation (i), we get x + 7 x 80 = 650 \(\Rightarrow\) x = 650 - 560 = 90 \(\therefore\)  Fixed expense for the party is Rs 90 (iv) (d): If there will be 15 guests, then amount that Mr Jindal has to pay = Rs (90 + 15 x 80) = Rs 1290 (v) (a): We have a 1  = 1, b 1  = 7, c 1  = -650 and  \(a_{2}=1, b_{2}=11, c_{2}=-970 \) \(\therefore \frac{a_{1}}{a_{2}}=1, \frac{b_{1}}{b_{2}}=\frac{7}{11}, \frac{c_{1}}{c_{2}}=\frac{-650}{-970}=\frac{65}{97}\) \(\text { Here, } \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) Thus, system of linear equations has unique solution.

(i) (a): Situation faced by Sudhir can be represented algebraically as 2x + 3y = 850 (ii) (b): Situation faced by Suman can be represented algebraically as 3x + 2y = 900 (iii) (c) : We have 2x + 3y = 850 .........(i) and 3x + 2y = 900 .........(ii) Multiplying (i) by 3 and (ii) by 2 and subtracting, we get 5y = 750 \(\Rightarrow\)   Y = 150 Thus, price of one Physics book is Rs 150. (iv) (d): From equation (i) we have, 2x + 3 x 150 = 850 \(\Rightarrow\) 2x = 850 - 450 = 400 \(\Rightarrow\) x = 200 Hence, cost of one Mathematics book = Rs 200 (v) (a): From above, we have \(a_{1} =2, b_{1}=3, c_{1}=-850 \) \(\text { and } a_{2} =3, b_{2}=2, c_{2}=-900\) \(\therefore \quad \frac{a_{1}}{a_{2}}=\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{3}{2}, \frac{c_{1}}{c_{2}}=\frac{-850}{-900}=\frac{17}{18} \Rightarrow \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) Thus system of linear equations has unique solution.

(i) (b): Algebraic representation of situation of day-I is 2x + y = 1600. (ii) (a): Algebraic representation of situation of day- II is 4x + 2y = 3000 \(\Rightarrow\) 2x + y = 1500. (iii) (c) : At x-axis, y = 0 \(\therefore\)   At y = 0, 2x + y = 1600 becomes 2x = 1600 \(\Rightarrow\) x = 800 \(\therefore\) Linear equation represented by day- I intersect the x-axis at (800, 0). (iv) (d) : At y-axis, x = 0 \(\therefore\) 2x + Y = 1500 \(\Rightarrow\)  y = 1500 \(\therefore\) Linear equation represented by day-II intersect the y-axis at (0, 1500). (v) (b): We have, 2x + y = 1600 and 2x + y = 1500 Since  \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \text { i.e., } \frac{1}{1}=\frac{1}{1} \neq \frac{16}{15}\) \(\therefore\) System of equations have no solution. \(\therefore\) Lines are parallel.

(i) (b): We have  \(6 x^{2}+x-2=0\) \(\Rightarrow \quad 6 x^{2}-3 x+4 x-2=0 \) \(\Rightarrow \quad(3 x+2)(2 x-1)=0 \) \(\Rightarrow \quad x=\frac{1}{2}, \frac{-2}{3}\) (ii) (c):  \(2 x^{2}+x-300=0\) \(\Rightarrow \quad 2 x^{2}-24 x+25 x-300=0 \) \(\Rightarrow \quad(x-12)(2 x+25)=0 \) \(\Rightarrow \quad x=12, \frac{-25}{2}\) (iii) (d):   \(x^{2}-8 x+16=0\) \(\Rightarrow(x-4)^{2}=0 \Rightarrow(x-4)(x-4)=0 \Rightarrow x=4,4\) (iv) (d):   \(6 x^{2}-13 x+5=0\) \(\Rightarrow \quad 6 x^{2}-3 x-10 x+5=0 \) \(\Rightarrow \quad(2 x-1)(3 x-5)=0 \) \(\Rightarrow \quad x=\frac{1}{2}, \frac{5}{3}\) (v) (a):  \(100 x^{2}-20 x+1=0\) \(\Rightarrow(10 x-1)^{2}=0 \Rightarrow x=\frac{1}{10}, \frac{1}{10}\)  

Number of pairs of shoes in 1 st , 2 nd , 3 rd row, ... are 3,5,7, ... So, it forms an A.P. with first term a = 3, d = 5 - 3 = 2 (i) (d): Let n be the number of rows required. \(\therefore S_{n}=120 \) \(\Rightarrow \quad \frac{n}{2}[2(3)+(n-1) 2]=120 \) \(\Rightarrow \quad n^{2}+2 n-120=0 \Rightarrow n^{2}+12 n-10 n-120=0\) \(\Rightarrow \quad(n+12)(n-10)=0 \Rightarrow n=10\) So, 10 rows required to put 120 pairs. (ii) (b): No. of pairs in 1ih row = t 17 = 3 + 16(2) = 35 No. of pairs in 10th row = t 10  = 3 + 9(2) = 21 \(\therefore\) Required difference = 35 - 21 = 14 (iii) (c) : Here n = 15 \(\therefore\) t 15  = 3 + 14(2) = 3 + 28 = 31 (iv) (a): No. of pairs in 30 th row = t 30 = 3 +29(2) = 61 (v) (c): No. of pairs in 5 th row = t 5  = 3 + 4(2) = 11 No. of pairs in 8 th row = t 8  = 3 + 7(2) = 17 \(\therefore\) Required sum = 11 + 17 = 28

Let the numbers on the cards be a, a + d, a + Zd, ... According to question, We have (a + 5d) + (a + 13d) = -76 \(\Rightarrow\) 2a+18d = -76 \(\Rightarrow\) a + 9d= -38 ... (1) And (a + 7d) + (a + 15d) = -96 \(\Rightarrow\) 2a + 22d = -96 \(\Rightarrow\) a + 11d = -48 ...(2) From (1) and (2), we get 2d= -10 \(\Rightarrow\) d= -5 From (1), a + 9(-5) = -38 \(\Rightarrow\) a = 7 (i) (b): The difference between the numbers on any two consecutive cards = common difference of the A.P.=-5 (ii) (d): Number on first card = a = 7 (iii) (b): Number on 19th card = a + 18d = 7 + 18(-5) = -83 (iv) (a): Number on 23rd card = a + 22d = 7 + 22( -5) = -103 (v) (d):  \(S_{15}=\frac{15}{2}[2(7)+14(-5)]=-420\)

(i) (c) (ii) (c) (iii) (d) (iv) (b) (v) (c)

Here S n = 0.1n 2 + 7.9n (i) (c): S n -1 = 0.1(n - 1) 2 + 7.9(n - 1) = 0.1n 2 + 7.7n - 7.8 (ii) (b): S 1 = t 1  = a = 0.1(1) 2 + 7.9(1) = 8 cm = Diameter of core So, radius of the core = 4 cm (iii) (a): S 2 = 0.1(2) 2 + 7.9(2) = 16.2 (iv) (d): Required diameter = t 2 = S 2 - S 1 = 16.2 - 8 = 8.2 cm (v) (c): As d = t 2 - t 1  = 8.2 - 8 = 0.2 cm So, thickness of tissue = 0.2 \(\div\)   2 = 0.1 cm = 1 mm

(i) (a): Speed = 1200 km/hr \(\text { Time }=1 \frac{1}{2} \mathrm{hr}=\frac{3}{2} \mathrm{hr}\) \(\therefore\)  Required distance = Speed x Time \(=1200 \times \frac{3}{2}=1800 \mathrm{~km}\) (ii) (c): Speed = 1500 km/hr Time =  \(\frac{3}{2}\)  hr. \(\therefore\)  Required distance = Speed x Time \(=1500 \times \frac{3}{2}=2250 \mathrm{~km}\) (iii) (b): Clearly, directions are always perpendicular to each other. \(\therefore \quad \angle P O Q=90^{\circ}\) (iv) (a): Distance between aeroplanes after  \(1\frac{1}{2}\)   hour  \(\begin{array}{l} =\sqrt{(1800)^{2}+(2250)^{2}}=\sqrt{3240000+5062500} \\ =\sqrt{8302500}=450 \sqrt{41} \mathrm{~km} \end{array}\) (v) (d): Area of  \(\Delta\) POQ= \(\frac{1}{2}\) x base x height \(=\frac{1}{2} \times 2250 \times 1800=2250 \times 900=2025000 \mathrm{~km}^{2}\)

(i) (b) (ii) (c): Using Pythagoras theorem, we have PQ 2 = PR 2 + RQ 2 \(\Rightarrow(26)^{2}=(2 x)^{2}+(2(x+7))^{2} \Rightarrow 676=4 x^{2}+4(x+7)^{2} \) \(\Rightarrow 169=x^{2}+x^{2}+49+14 x \Rightarrow x^{2}+7 x-60=0\) \(\Rightarrow x^{2}+12 x-5 x-60=0 \) \(\Rightarrow x(x+12)-5(x+12)=0 \Rightarrow(x-5)(x+12)=0 \) \(\Rightarrow x=5, x=-12\) \(\therefore \quad x=5\)   [Since length can't be negative] (iii) (a) : PR = 2x = 2 x 5 = 10 km (iv) (b): RQ= 2(x + 7) = 2(5 + 7) = 24 km (v) (d): Since, PR + RQ = 10 + 24 = 34 km Saved distance = 34 - 26 = 8 km

(i) (b): If \(\Delta\) AED and \(\Delta\) BEC, are similar by SAS similarity rule, then their corresponding proportional sides are  \(\frac{B E}{A E}=\frac{C E}{D E}\) (ii) (c): By Pythagoras theorem, we have \(\begin{array}{l} B C=\sqrt{C E^{2}+E B^{2}}=\sqrt{4^{2}+3^{2}}=\sqrt{16+9} \\ =\sqrt{25}=5 \mathrm{~cm} \end{array}\) (iii) (a): Since \(\Delta\) ADE and \(\Delta\) BCE are similar. \(\therefore \quad \frac{\text { Perimeter of } \triangle A D E}{\text { Perimeter of } \Delta B C E}=\frac{A D}{B C} \) \(\Rightarrow \frac{2}{3}=\frac{A D}{5} \Rightarrow A D=\frac{5 \times 2}{3}=\frac{10}{3} \mathrm{~cm}\) (iv) (b): \(\frac{\text { Perimeter of } \triangle A D E}{\text { Perimeter of } \Delta B C E}=\frac{E D}{C E} \) \(\Rightarrow \frac{2}{3}=\frac{E D}{4} \Rightarrow E D=\frac{4 \times 2}{3}=\frac{8}{3} \mathrm{~cm}\) (v) (d) :   \(\frac{\text { Perimeter of } \Delta A D E}{\text { Perimeter of } \Delta B C E}=\frac{A E}{B E} \Rightarrow \frac{2}{3} B E=A E\) \(\Rightarrow A E=\frac{2}{3} \sqrt{B C^{2}-C E^{2}} \) \(\text { Also, in } \triangle A E D, A E=\sqrt{A D^{2}-D E^{2}}\)

(i) (a): We have, OA = 2 \(\sqrt{2}\) km \(\Rightarrow \sqrt{2^{2}+y^{2}}=2 \sqrt{2} \) \(\Rightarrow 4+y^{2}=8 \Rightarrow y^{2}=4 \) \(\Rightarrow y=2 \quad(\because y=-2 \text { is not possible })\) (ii) (c): We have OB = 8 \(\sqrt{2}\) \(\Rightarrow \sqrt{x^{2}+8^{2}}=8 \sqrt{2} \) \(\Rightarrow x^{2}+64=128 \Rightarrow x^{2}=64 \) \(\Rightarrow x=8 \quad(\because x=-8 \text { is not possible })\) (iii) (c) : Coordinates of A and Bare (2, 2) and (8, 8) respectively, therefore coordinates of point M are \(\left(\frac{2+8}{2}, \frac{2+8}{2}\right)\) i.e .,(5.5) (iv) (d): Let A divides OM in the ratio k: 1.Then \(2=\frac{5 k+0}{k+1} \Rightarrow 2 \mathrm{k}+2=5 k \Rightarrow 3 k=2 \Rightarrow k=\frac{2}{3}\) \(\therefore\) Required ratio = 2 : 3 (v) (b): Since M is the mid-point of A and B therefore AM = MB. Hence, he should try his luck moving towards B.

(i) (c): Required coordinates are  \(\left(0, \frac{4}{3}\right)\) (ii) (c) (iii) (a): Radius = Distance between (0,0) and  \(\left(\frac{4}{3}, 0\right)\) \(=\sqrt{\left(\frac{4}{3}\right)^{2}+0^{2}}=\frac{4}{3} \text { units }\) (iv) (b): Area of circle = \(\pi\) (radius) 2 \(=\pi\left(\frac{4}{3}\right)^{2}=\frac{16}{9} \pi \text { sq. units }\) (v) (d): Let the coordinates of the other end be (x,y). Then (0,0) will bethe mid-point of  \(\left(1, \frac{\sqrt{7}}{3}\right)\)  and (x, y). \(\therefore\left(\frac{1+x}{2}, \frac{\frac{\sqrt{7}}{3}+y}{2}\right)=(0,0) \) \(\Rightarrow \frac{1+x}{2}=0 \text { and } \frac{\frac{\sqrt{7}}{3}+y}{2}=0 \) \(\Rightarrow x=-1 \text { and } y=-\frac{\sqrt{7}}{3}\) Thus, the coordinates of other end be  \(\left(-1, \frac{-\sqrt{7}}{3}\right)\)

Coordinates of A, Band Care (-2, -3), (2, 3) and (3,2). (i) (d): Required distance  \(=\sqrt{(2+2)^{2}+(3+3)^{2}}\) \(=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=2 \sqrt{13} \mathrm{~km} \approx 7.2 \mathrm{~km}\) (ii) (d): Required distance  \(=\sqrt{(3+2)^{2}+(2+3)^{2}}\) \(=\sqrt{5^{2}+5^{2}}=5 \sqrt{2} \mathrm{~km}\) (iii) (b): Distance between Band C \(=\sqrt{(3-2)^{2}+(2-3)^{2}}=\sqrt{1+1}=\sqrt{2} \mathrm{~km}\) Thus, distance travelled by first bus to reach to B \(=A C+C B=5 \sqrt{2}+\sqrt{2}=6 \sqrt{2} \mathrm{~km} \approx 8.48 \mathrm{~km}\) and distance travelled by second bus to reach to B \(=A B=2 \sqrt{13} \mathrm{~km} \approx 7.2 \mathrm{~km}\) \(\therefore\)  Distance of first bus is greater than distance of the second bus, therefore second bus should be chosen. (iv) (d): Distance travelled by first bus = 8.48 km \(\therefore\) Total fare = 8.48 x 10 = Rs 84.80 (v) (b): Distance travelled by second bus = 7. 2 km \(\therefore\) Total fare = 7.2 x 15 = Rs 108  

Related 10th Standard CBSE Maths Materials

10th standard cbse syllabus & materials, cbse 10th social science the making of a global world chapter case study question with answers, cbse 10th social science nationalism in india chapter case study question with answers, cbse 10th social science the rise of nationalism in europe chapter case study question with answers, cbse 10th science metals and non metals chapter case study question with answers, cbse 10th science acids, bases and salts chapter case study question with answers, cbse 10th science chemical reactions and equations chapter case study question with answers, class 10th science - our environment case study questions and answers 2022 - 2023, class 10th science - magnetic effects of electric current case study questions and answers 2022 - 2023, class 10th science - electricity case study questions and answers 2022 - 2023, class 10th science - human eye and the colourful world case study questions and answers 2022 - 2023, class 10th science - light reflection and refraction case study questions and answers 2022 - 2023, class 10th science - heredity and evolution case study questions and answers 2022 - 2023, class 10th science - how do organisms reproduce case study questions and answers 2022 - 2023, class 10th science - life processes case study questions and answers 2022 - 2023, class 10th science - periodic classification of elements case study questions and answers 2022 - 2023.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

10th Standard CBSE Study Materials

10th Standard CBSE Subjects

• Class 10 Notes
• 9th IT CODE 402
• 10th IT CODE 402
• 10th Hindi Grammar MCQ
• 9th Hindi Grammar MCQ

Case Study Questions Class 10 Maths with Solutions PDF Download

 case study questions class 10 maths pdf, case study questions class 10 maths with solutions, case study questions class 10 maths cbse chapter wise pdf download, how to solve case-based question in maths.

• First of all, a student needs to read the complete passage thoroughly. Then start solving the question
• After reading the question try to understand from which topics the question is asked. and try to remember all the concepts of that topic.
• Sometimes the question is very tricky and you will find it very difficult to understand. In that case, Read the question and passage again and again.
• After solving the answer check your answer with the options given.
• Remember, write only answering your answer book

Link to Download Case-Study Questions of class 10

Post a comment, popular posts.

Information Technology Code 402 Class 10 Notes 2023

Class 10 Hindi Vakya Bhed MCQ | Term 1 - CBSE 2022

Pad Parichay Class 10 MCQ | CBSE - 2022 | पद परिचय

Class 10 Hindi Samas MCQ Questions - CBSE 2022 Term 1

Information Technology Code 402 Class 10 Solutions

Set-1 | Padbandh MCQ Questions Class 10 - CBSE 2022

Class 10 Hindi Vyakaran Vachya MCQ Question - CBSE 2023

Menu footer widget.

• Privacy Policy